- Révisions générales
- Ensembles de nombres
- Manipulations standards
- Fonctions usuelles
- Trigonométrie
- Notations Somme et Produit
- Limite
- Dérivabilité
- Développements limités
- Dérivées partielles
Octobre 2019 - Promo Fluor
Plan du cours (S1)
Objectifs
- Connaître quelques propriétés de \(\mathbb{N}\), \(\mathbb{Q}\) et \(\mathbb{R}\)
- Savoir manipuler des puissances (en particulier avec \(e^x\) et \(\ln{x}\))
- Savoir résoudre des équations et des inéquations
- Connaître les valeurs et les identités remarquables en trigonométrie
- Utiliser les fonctions trigonométriques inverses
- Manipuler les notations somme et produit
Les ensembles de nombres
Les nombres
On rappelle l’existence de d’ensembles de nombres déjà vu dans les classes antérieures:
- \(\mathbb{N}\): les entiers naturels (entiers positifs)
- \(\mathbb{Z}\): les entiers relatifs (entiers positifs et leurs opposés)
- \(\mathbb{Q}\): les rationnels (fractions d’entiers)
- \(\mathbb{R}\): les nombres réels (tous ceux qui peuvent apparaître comme la mesure de quelques chose et leurs opposés). La majorité des nombres réels ne sont pas rationnels: \(\sqrt{2}, \pi, e\).
- \(\mathbb{C}\): les nombres complexes (très utiles pour factoriser des polynômes ou représenter des courants électromagnétiques)
La factorielle
La
\[n! = 1 \times 2 \times \dots \times (n-1) \times n\]
Par convention, \(0! = 1\).
Remarque On note que \(n! = n \times (n-1)!\).
La factorielle (II)
On donne ici les valeurs de \(n!\) pour de faibles valeurs de \(n\)
| n | factorielle |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5040 |
Le principe de récurrence (classique)
- \(P(n_0)\) est vraie. [Initialisation]
- \(\forall n \geq n_0, P(n) \rightarrow P(n+1)\) [Hérédité]
Alors \(\forall n \geq n_0, P(n)\) est vraie
Soit \(n\) un entier naturel non nul, trouver une formule close (c’est à dire sans \(\dots\)) et la démontrer pour
\(S_n = \frac{1}{2!} + \frac{2}{3!} + \dots + \frac{n-1}{n!} + \frac{n}{(n+1)!}\)
Parité, imparité et division euclidienne
Tout nombre entier \(n\) est soit pair, soit impair.
- Si \(n\) est pair, il existe un unique entier \(p\) tel que \(n = 2p\)
- Si \(n\) est impair, il existe un unique entier \(p\) tel que \(n = 2p+1\)
Généralisation (division euclidienne)
Pour tout entier naturel \(n\) et tout entier naturel non num \(d\), il existe un unique couple d’entiers \((q, r)\) tel que: \[ n = dq + r \text{ et } 0 \leq r \leq d-1 \] \(n\) est divisible par \(d\) si et seulement si \(r = 0\).
Montrer par récurrence que \((q,r)\) existe et par l’absurde qu’il est unique.
Nombres réels
-
Justifier l’existence d’un nombre réel dont le carré est égal à 2. À quelle
mesure correspond-il? - Montrer (par l’absurde) que \(\sqrt{2}\) n’est pas rationnel. On pourra commencer par démontrer que \(p^2\) est pair si et seulement si \(p\) est pair
- Généraliser et montrer que \(\sqrt{p}\) est irrationnel dès que \(p\) est premier
Remarque
\(\sqrt{2}, \pi, e\) sont des nombres irrationnels. La nécessité de construire \(\mathbb{R}\) provient de raisons non-algébriques, pour manipuler des quantités d’intérêt (en géométrie pour \(\sqrt{2}\) et \(\pi\), en calculs d’intérêts pour \(e\)) qu’on ne peut pas exprimer comme des fractions d’entiers.
Intervalle réel
Remarque Un intervalle est un sous-ensemble de \(\mathbb{R}\) sans “trous”, sans discontinuité.
Il y a 3 types d’intervalles:
- ouvert: \(]a, b[ = \{ x \in \mathbb{R} \quad \text{tels que} \quad a < x < b \}\) avec \(a\) et \(b\) dans \(\mathbb{R} \cup \{-\infty, +\infty\}\)
- semi-ouvert: \([a, b[ = \{ x \in \mathbb{R} \quad \text{tels que} \quad a \leq x < b \}\) avec \(a \in \mathbb{R}\) et \(b \in \mathbb{R} \cup \{+\infty\}\) ou \(]a, b]\) avec des contraintes sumilaires.
- fermés: \([a, b] = \{ x \in \mathbb{R} \quad \text{tels que} \quad a \leq x \leq b \}\) avec \(a\) et \(b\) dans \(\mathbb{R}\)
Quelques propriétés de \(\mathbb{R}\) (optionnel)
Majorant, minorant (optionnel)
Un sous ensemble \(A \subset \mathbb{R}\) est dit
Si \(A\) est à la fois majorée et minorée, elle est
Intuitivement:
- \(M\) est plus grand que tous les nombres de \(A\)
- \(m\) est plus petit que tous les nombres de \(A\)
Majorant, minorant (exercices)
Traduire avec des quantificateurs les deux propositions suivantes:
- \(A\) n’est pas majorée.
- \(A\) n’est pas minorée.
Est-ce possible si \(A\) est fini? Pourquoi?
Borne supérieure, inférieure (optionnel)
Si \(M\) majore \(A\), alors tout \(x \geq M\) aussi. On cherche le plus petit majorant.
Soit \(A\) une partie
- \(A\) admet une
borne supérieure s’il existe \(M_0\) réel tel que- \(M_0\) est un majorant de \(A\)
- Tout majorant \(M\) de \(A\) vérifie \(M \geq M_0\)
- \(A\) admet une
borne inférieure s’il existe \(m_0\) réel tel que- \(m_0\) est un minorant de \(A\)
- Tout minorant \(m\) de \(A\) vérifie \(m \leq m_0\)
Si \(A\) admet une borne supérieure (resp. inférieure), alors elle est unique. On la note \(\sup A\) (resp. \(\inf A\)).
Borne supérieure, inférieure [admis]
-
Si \(A\) est
majorée , elle admet une borne supérieure. -
Si \(A\) est
minorée , elle admet une borne inférieure.
- La borne supérieure \(\sup A\) est-elle systématiquement un élément de \(A\)?
- Même question pour \(\inf A\)?
Maximum, Minimum (optionnel)
-
Soit \(A\) une partie majorée de \(\mathbb{R}\). Si \(\sup A\) est un élément de \(A\), on dit que \(\sup A\) est le
maximum de \(A\), noté \(\max A\). -
Soit \(A\) une partie minorée de \(\mathbb{R}\). Si \(\inf A\) est un élément de \(A\), on dit que \(\inf A\) est le
minimum de \(A\), noté \(\min A\).
Questions - Quelles parties de \(\mathbb{R}\) admettent un maximum? un minimum?
Réponses partielles
- Toute partie finie de \(\mathbb{R}\) admet un maximum et un minimum
- Toute partie majorée (resp. minorée) de \(\mathbb{Z}\) admet un maximum (resp. un minimum). Mais ce n’est plus vrai avec \(\mathbb{Q}\).
Opérations standards
Manipulations standards
À connaitre
- Développer / Factoriser
- Identités remarquables
- Manipulation de puissances (\(e^x\) et \(\ln\))
- Trigonométrie
Interdit
- Diviser par \(0\)
- Racine d’un nombre négatif
- logarithme d’un nombre négatif ou nul
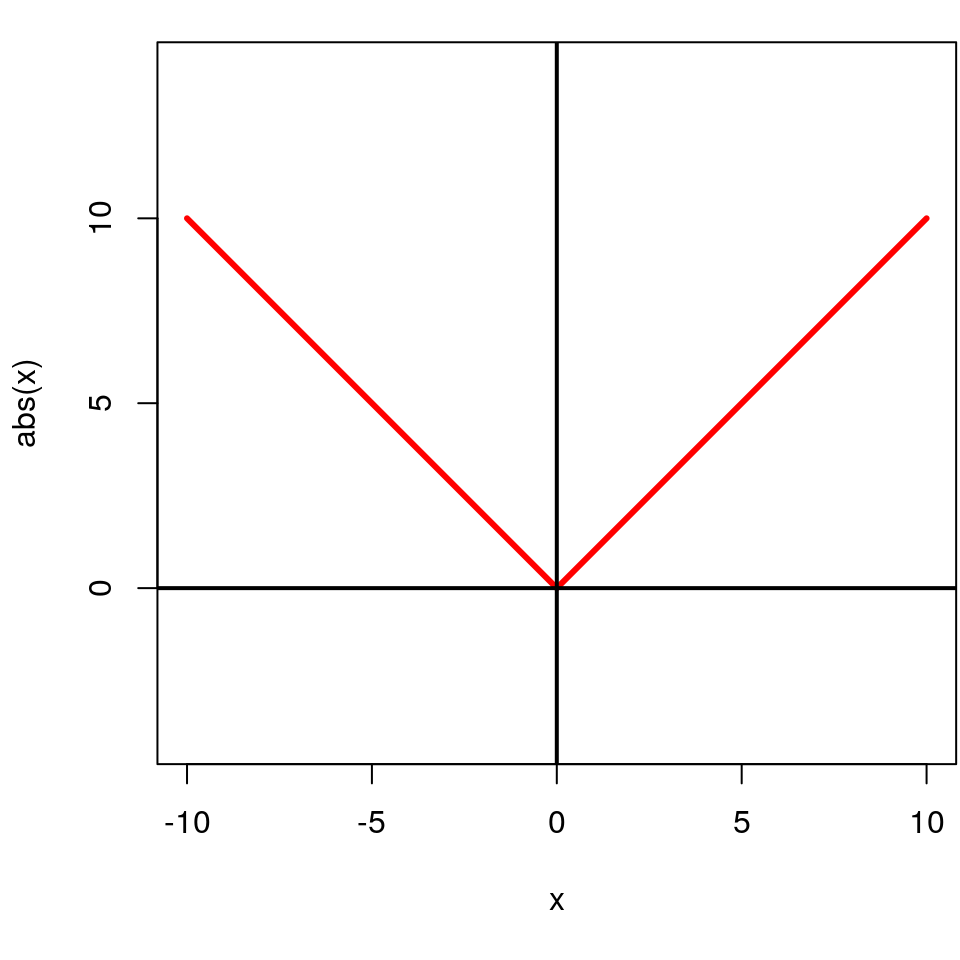
Valeur absolue
Soit \(x \in \mathbb{R}\), la valeur absolue de \(x\), notée \(|x|\) est définie par \[|x| = \max(x, -x)\]
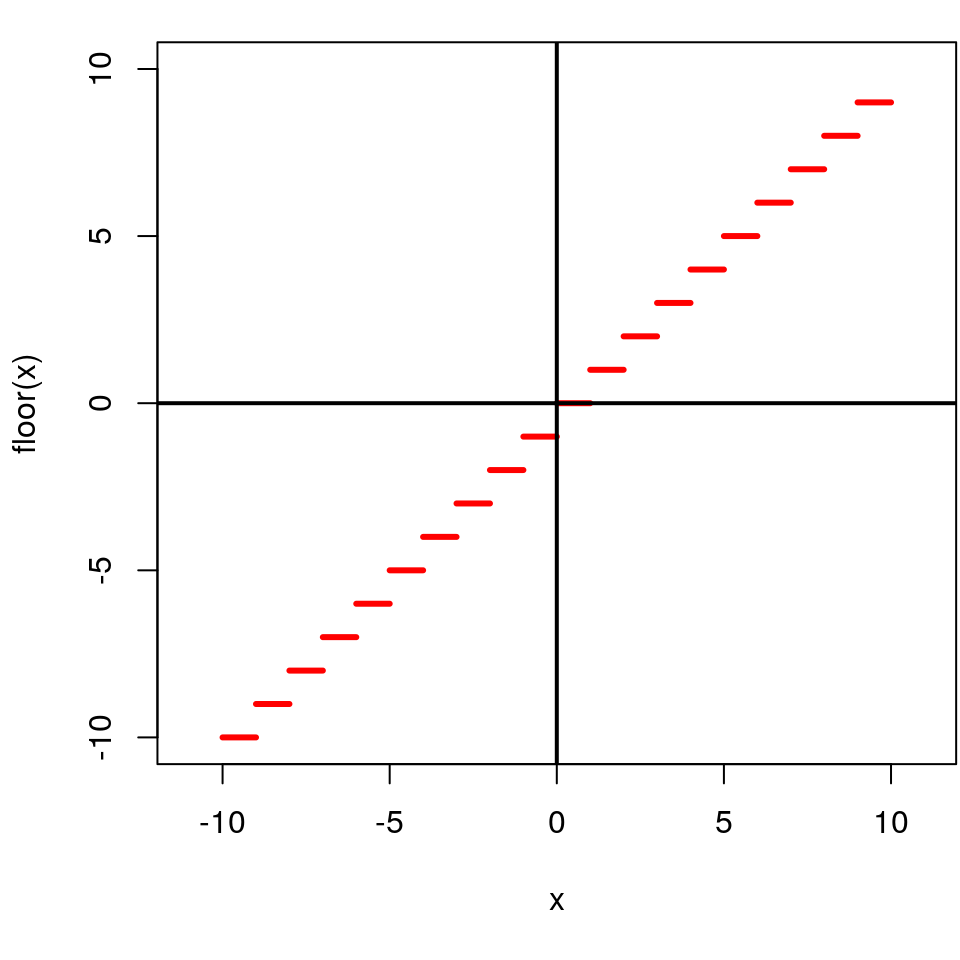
Partie Entière
Soit \(x \in \mathbb{R}\), la partie entière de \(x\), notée \(\lfloor x \rfloor\) est définie par \[\lfloor x \rfloor \in \mathbb{Z} \quad \text{et} \quad \lfloor x \rfloor \leq x < \lfloor x \rfloor + 1\]
Valeur absolue et partie entière: exercices
Simplifier les expressions suivantes:
- \(\lfloor \pi \rfloor\),
- \(\lfloor 0.99 \rfloor\), \(\lfloor 1 \rfloor\), \(\lfloor 1.01 \rfloor\)
- \(\lfloor -0.99 \rfloor\), \(\lfloor -1 \rfloor\), \(\lfloor -1.01 \rfloor\)
Résoudre les équations d’inconnue \(x\) suivantes:
- \(\lfloor 2x + 1 \rfloor= 3\).
- \(|2x + 1| = 3\)
Puissance
Pour \(a > 0\) et \(x \in \mathbb{R}\), on pose \(a^x = e^{x \ln a}\)
Soient \(x, y\) deux rééls et \(a, b\) deux réels strictement positifs:
| \(a^0 = 1\) | \(a^{x+y} = a^x . a^y\) | \((a)^{-x} = \frac{1}{a^x}\) |
| \(a^{x -y} = \frac{a^x}{a^y}\) | \((ab)^{x} = (a)^x . (b)^x\) | \((a^x)^y = a^{x.y}\) |
| \(a^1 = a\) | \((a^x)^{\frac{1}{x}} = a\) | \(\sqrt[n]{a} = a^{\frac{1}{n}}\) |
Puissance (II)
Rapppels
- Si \(a > 0\), \(\sqrt[n]{a}\) est l’unique réel positif tel que \((\sqrt[n]{a})^n = a\).
- Pour tout réel \(x\), \(\sqrt{x^2} = |x|\) (et non pas \(x\)). La racine carrée est positive.
Équations
Il y a deux grandes types d’équations:
- les polynômiales
- les autres
Pour les polynömiales, il faut savoir résoudre des équations de degré \(1\) et \(2\) et factoriser à partir de racines évidentes pour les celles de degrés supérieures. Pour les autres, il faut utiliser des astuces ad-hoc (mais avec quelques astuces classiques dont le changement de variables).
En présence de paramètres, il faut parfois faire des disjonctions de cas pour éviter de faire des opérations interdites.
Équations à paramètres
Résoudre, en fonction des paramètres \(a\) et \(b\), les équations suivantes:
- \(ax = b\)
- \(ax +b = bx +a\)
- \(e^x = a\)
- \(ax^2 - 2bx + 2 = 0\)
Équations polynômiales
Résoudre les équations (de \(X\)) suivantes:
- \(X^3 - X^2 + X - 1 = 0\)
- \(X^4 + X^2 - 1 = 0\).
Équations non-polynômiales
Résoudre les équations (de \(x\)) suivantes:
- \(3x^4 + 5x^2 - 2 = 0\)
- \((\ln x)^2 + 3\ln x + 2 = 0\)
- \(x = \sqrt{x} + 2\)
- \(e^x - e^{-x} = 2\)
- \(x^2 - 3x + 4 + \frac{8 - 6x}{x^2 - 2} = 0\)
Inégalités
Soient \(a\) et \(b\) deux réels tels que \(a \leq 5\) et \(b \leq 6\). Que peut-on dire de \(2a\), \(-3b\), \(a+b\), \(a - b\), \(ab\), \(a/b\)? Même chose si \(b \geq 6\).
Inégalités: Règles de manipulation
- \(a \geq b\) équivaut à \(-a \leq -b\) [changement de signe]
Si \(a\) et \(b\) ont même signe , \(a \leq b\) équivaut à \(\frac{1}{a} \geq \frac{1}{b}\)- On peut additionner des égalités de
même sens : si \(a \leq b\) et \(c \leq d\) alors \(a+c \leq b+d\). - Si \(a, b, c, d\) sont
positifs , on peut multiplier des inégalités: si \(a \leq b\) et \(c \leq d\) alors \(ac \leq bd\) - Si \(f\) est une fonction
croissante sur un intervalle \(I \subset \mathbb{R}\) et \(a\) et \(b\) sont des éléments de \(I\) tels que \(a \leq b\), alors \(f(a) \leq f(b)\). - Si \(f\) est une fonction
décroissante sur un intervalle \(I \subset \mathbb{R}\) et \(a\) et \(b\) sont des éléments de \(I\) tels que \(a \leq b\), alors \(f(a) \geq f(b)\).
Inégalité triangulaire et arithmético-géométrique
Pour tous réels \(x\) et \(y\), \(|x + y| \leq |x| + |y|\).
Cette égalité vient de la géométrie: dans un triangle, la sommes des longueurs de deux côtés est toujours supérieure ou égale à celle du troisième (avec égalité si et seulement si le triangle est aplati).
Montrer que pour tous réels \(x\) et \(y\), \(| |x| - |y| | \leq |x - y|\).
Montrer que pour tous réels \(x\) et \(y\), \(x^2 + y^2 \geq 2|xy|\). [inégalité arithmético-géométrique, à connaître]
Inégalités: Mise en oeuvre
Résoudre les inégalités suivantes:
- \(\ln(3x) \leq \ln(2x)\)
- \(3.2^{3x-4} \geq 7^8\)
- \(5\left( \frac{1}{3} \right)^{x} \leq 10^{-10}\)
- \(\sqrt{x} \geq x + 1\)
Rappels de trigonométrie
Trigonométrie: les bases (I)
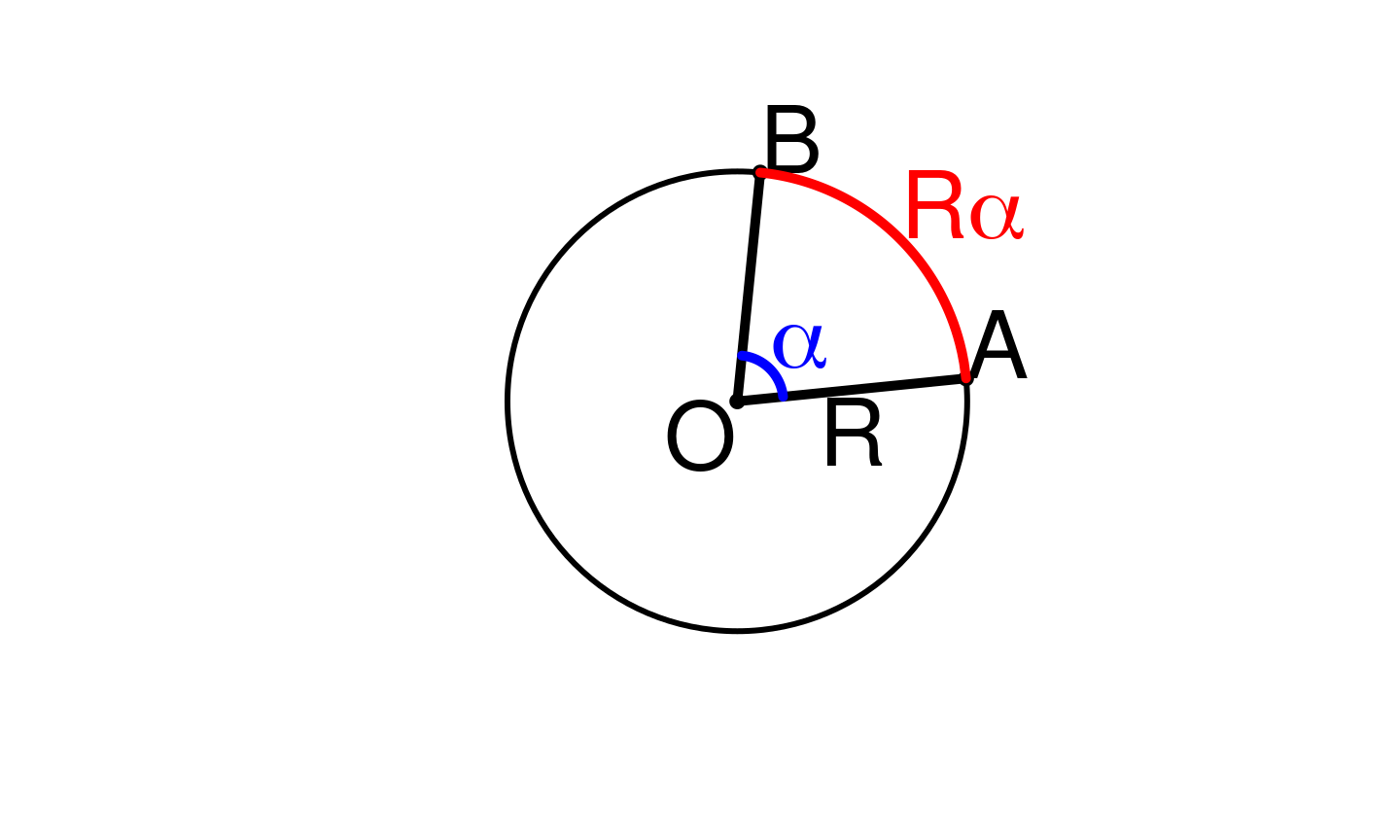
La mesure en radians d’un angle \(\alpha\) est la longueur d’un arc de cercle de rayon \(1\) délimité par cet angle.
Plus généralement, soit \(\mathcal{C}\) est un cercle de centre \(O\) et de rayon \(R\). On considère deux points \(A\) et \(B\) de \(\mathcal{C}\).
La mesure principale de l’angle \(\hat{AOB}\) est l’unique réel \(\alpha\) tel que
- \(\alpha \in [0, 2\pi [\)
- la longeur de l’arc de cercle délimité par le secteur angulaire \(\hat{AOB}\) est \(R\alpha\), et son aire est \(\frac{\alpha}{2}R^2\)
Trigonométrie: les bases (II)
Trigonométrie: angle orienté
Du point de vue des longueurs (positives par définition), on a le choix de “tourner” dans un sens ou dans l’autre. Dans de nombreux cas, la question du “sens” de rotation est néanmoins importante.
Par définition, on décide que le sens positif est le sens contraire à celui des aiguilles d’une montre. C’est le
Trigonométrie: angle orienté (II)
Soient \(A, B, C\) 3 points du plan, l’angle orienté \(\hat{ABC}\) est noté \((\vec{BA}, \vec{BC})\).
Plus généralement, pour tous vecteurs \(\vec{u}\), \(\vec{v}\) du plan, on note \((\vec{u}, \vec{v})\) l’angle orienté \((\vec{BA}, \vec{BC})\) pour tous points \(A, B, C\) tels que \(\vec{u} = \vec{BA}\) et \(\vec{v} = \vec{BC}\)
Rotation de centre Ω et d’angle α
Soit \(\mathcal{P}\) le plan usuel orienté. Soit \(\Omega\) un point du plan et \(\alpha\) un réel. On appelle
- \(|\Omega M| = |\Omega M'|\)
- \((\vec{\Omega M}, \vec{\Omega M'}) = \alpha\)
Définition géométrique
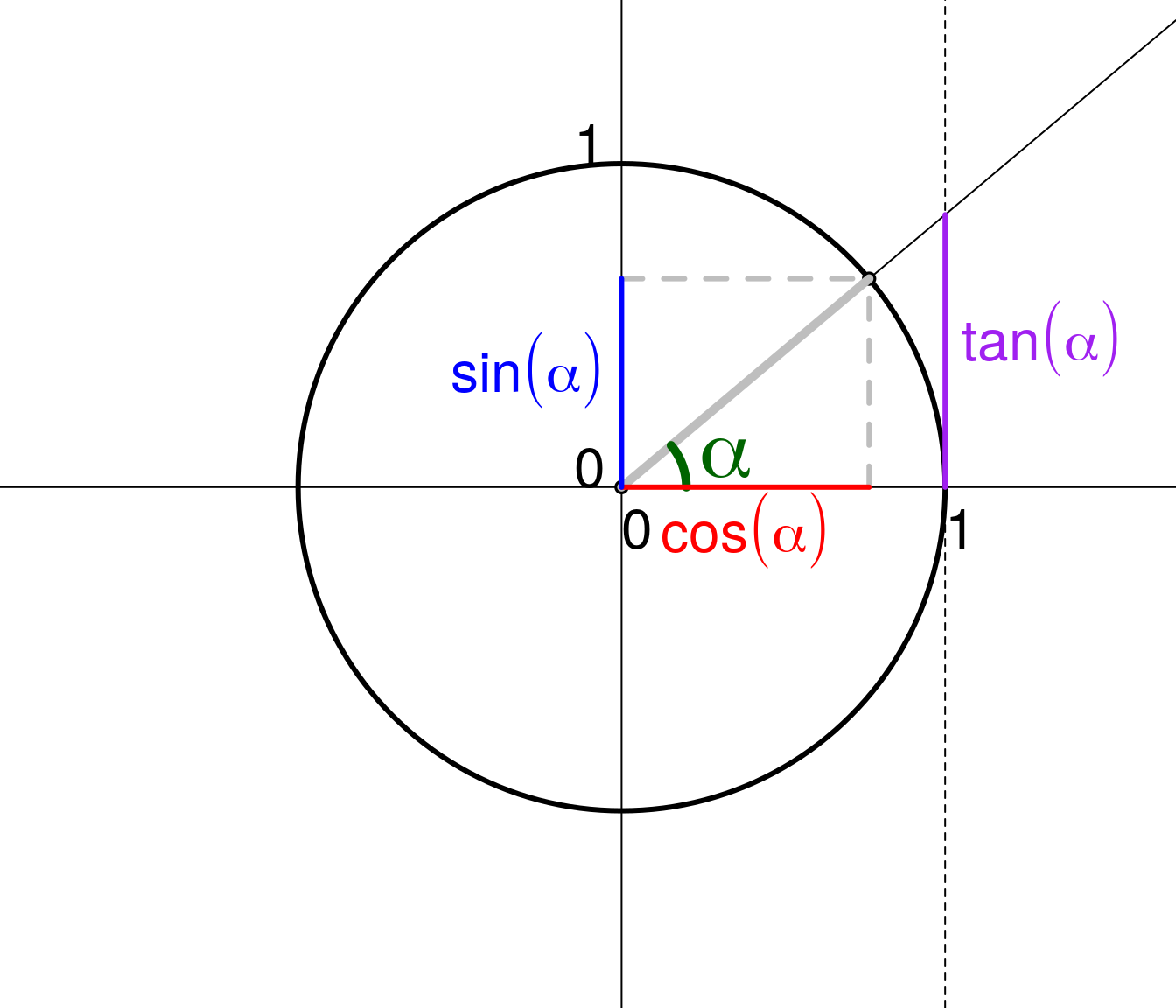
Propriété fondamentale de sinus et cosinus
- Soit \(\theta \in \mathbb{R}\), on a \(\cos^2 \theta + \sin^2 \theta = 1\)
- Réciproquement, pour tout couple \((\alpha, \beta)\) de nombres réels tels que \(\alpha^2 + \beta^2 = 1\), il existe un réel \(\theta\) tel que \(\alpha = \cos(\theta)\) et \(\beta = \sin(\theta)\).
Les deux propriétés traduisent le fait que le point \(M\) de coordonnées \((\alpha, \beta)\) est sur le cercle trignométrique (celui de centre \(O = (0, 0)\) et de rayon \(1\)).
Valeurs remarquables (à connaître…)
- Pour tout \(k \in \mathbb{Z}\), \(\cos(k\pi) = (-1)^k\), \(\sin(k\pi) = \tan(k\pi) = 0\)
- Pour tout \(k \in \mathbb{Z}\), \(\cos(\pi/2 + k\pi) = 0\), \(\sin(\pi/2 + k\pi) = (-1)^k\) et \(\tan(\pi/2 + k\pi)\) n’est pas défini.
- \(\cos(\pi/3) = \sin(\pi/6) = \frac{1}{2}\)
- \(\cos(\pi/6) = \sin(\pi/3) = \frac{\sqrt{3}}{2}\)
- \(\cos(\pi/4) = \sin(\pi/4) = \frac{\sqrt{2}}{2}\)
- \(\tan(\pi/3) = \frac{1}{\tan(\pi/6)} = \sqrt{3}\)
- \(\tan(\pi/4) = 1\).
Formules d’additions
Seules les deux premières sont nécessaires, les autres s’en déduisent.
Pour tout couple de réels \((a, b)\), on a:
- \(\cos(a+b) = \cos(a)\cos(b) - \sin(a)\sin(b)\) \(\sin(a+b) = \sin(a)\cos(b) + \cos(a)\sin(b)\)
- \(\cos(a-b) = \cos(a)\cos(b) + \sin(a)\sin(b)\)
- \(\sin(a-b) = \sin(a)\cos(b) - \cos(a)\sin(b)\)
Et sous réserve que les tangentes soient bien définies
- \(\tan(a+b) = \frac{\tan(a) + \tan(b)}{1 - \tan(a)\tan(b)}\)
- \(\tan(a-b) = \frac{\tan(a) - \tan(b)}{1 + \tan(a)\tan(b)}\)
Formules de factorisation
Elles se démontrent à partir des formules d’addition (voir feuille d’exercice)
Pour tout couple de réels \((a, b)\), on a:
- \(\cos(a) + \cos(b) = 2\cos\left(\frac{a+b}{2}\right)\cos\left(\frac{a-b}{2}\right)\)
- \(\sin(a) + \sin(b) = 2\sin\left(\frac{a+b}{2}\right)\cos\left(\frac{a-b}{2}\right)\)
En cas de doute, n’hésitez pas à tester ces formules sur des valeurs connues (par exemple \(a = b\) ou \(a = -b\)) pour vérifier que vous avez la bonne formule. .
Angles doubles
Le cas \(a=b\) correspond à un cas particulier d’intérêt (appelé angle double). Les formules d’additions se simplifient alors en
- \(\cos(2a) = \cos^2(a) - \sin^2(a) = 2\cos^2(a) - 1 = 1 - 2\sin^2(a)\)
- \(\sin(2a) = 2\sin(a)\cos(a)\)
- \(\tan(2a) = \frac{2\tan(a)}{1 - \tan^2(a)}\)
Équations trigonométriques (I)
Soit \(u\) un réel donné, on cherche à résoudre en \(x\):
- \(\cos(u)=\cos(x)\)
\(x\) est solution \(\Leftrightarrow \begin{cases} \exists k\in \mathbb{Z} \text{ tel que } x = u + 2k\pi \\ \text{OU} \\ \exists k\in \mathbb{Z} \text{ tel que } x = -u + 2k\pi\end{cases}\)
- \(\sin(u)=\sin(x)\)
\(x\) est solution \(\Leftrightarrow \begin{cases} \exists k\in \mathbb{Z} \text{ tel que } x = u + 2k\pi \\ \text{OU} \\ \exists k\in \mathbb{Z} \text{ tel que } x = \pi-u + 2k\pi\end{cases}\)
Attention à ne pas oublier le OU du système.
Équations trigonométriques fondamentales (II)
Soit \(u\) un réel donnéon cherche à résoudre en \(x\).
- \(\tan(u)=\tan(x)\) (où \(u\) n’est pas de la forme \(\pi/2 + k\pi\))
\(x\) est solution si et seulement si \(\exists k\in \mathbb{Z}\) tel que \(x = u + k\pi\)
- \(\sin(u)=\sin(x)\) ET \(\cos(u)=\cos(x)\)
\(x\) est solution si et seulement si \(\exists k\in \mathbb{Z}\) tel que \(x = u + 2k\pi\)
À retenir
- La donnée de \(\cos(x)\), \(\sin(x)\) ou \(\tan(x)\) ne permet pas de complétement caractériser \(x\)
- La donnée de \(\cos(x)\) et \(\sin(x)\) permet de bien caractériser \(x\)…
- …mais il reste toujours une infinité de solutions (égales à \(2\pi\) près).
Applications
Résoudre les équations suivantes:
- \(\cos(x) = \frac{1}{2}\)
- \(\sin(2x) = \frac{\sqrt{3}}{2}\)
- \(\tan(3x) = 1\)
Fonctions trigonométrique inverse
Fonctions trigonométriques inverses
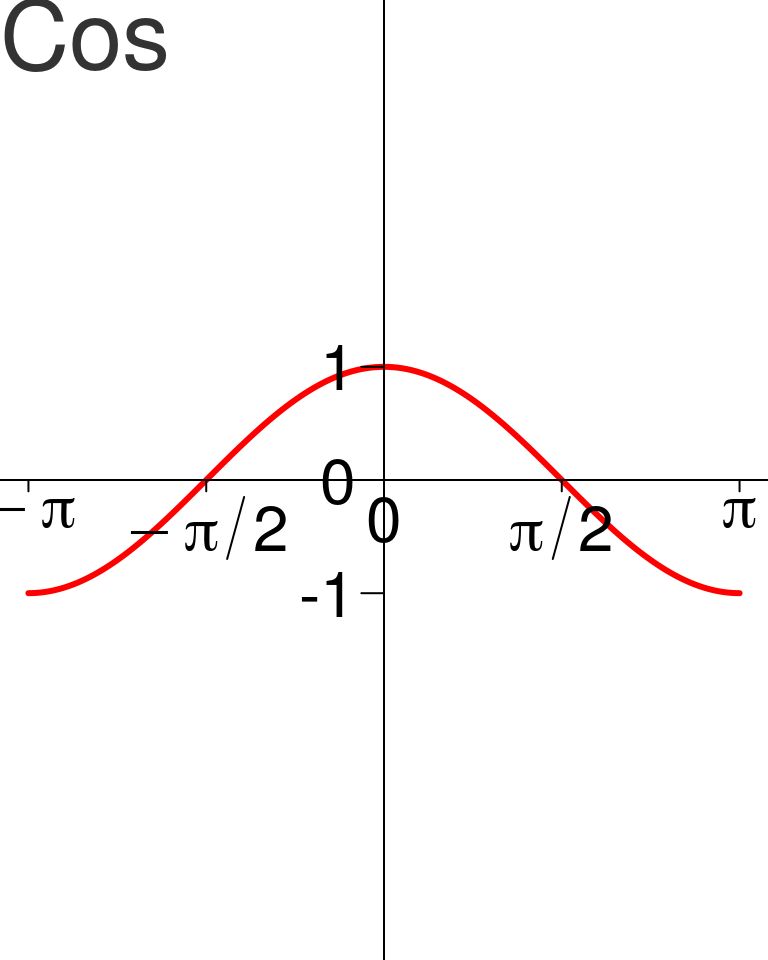
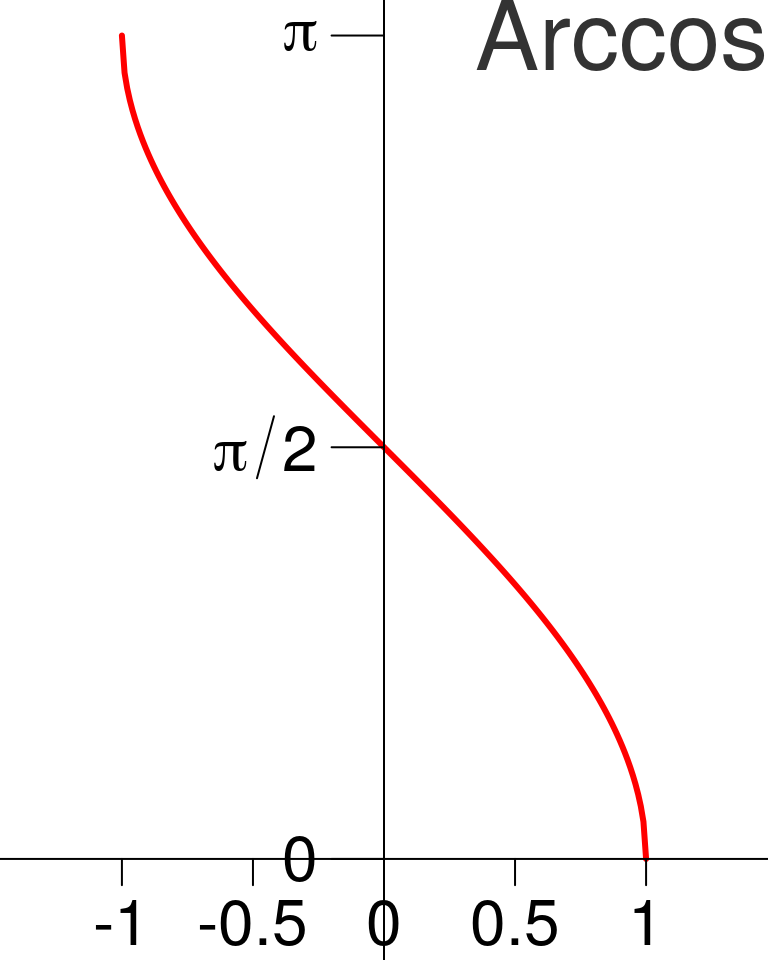
- Pour tout réel \(x \in [-1, 1]\), l’équation d’inconnue \(\theta\) \(\cos(\theta) = x\) admet une unique solution dans \([0, \pi]\). Cette solution est appelée \(\arccos(x)\).
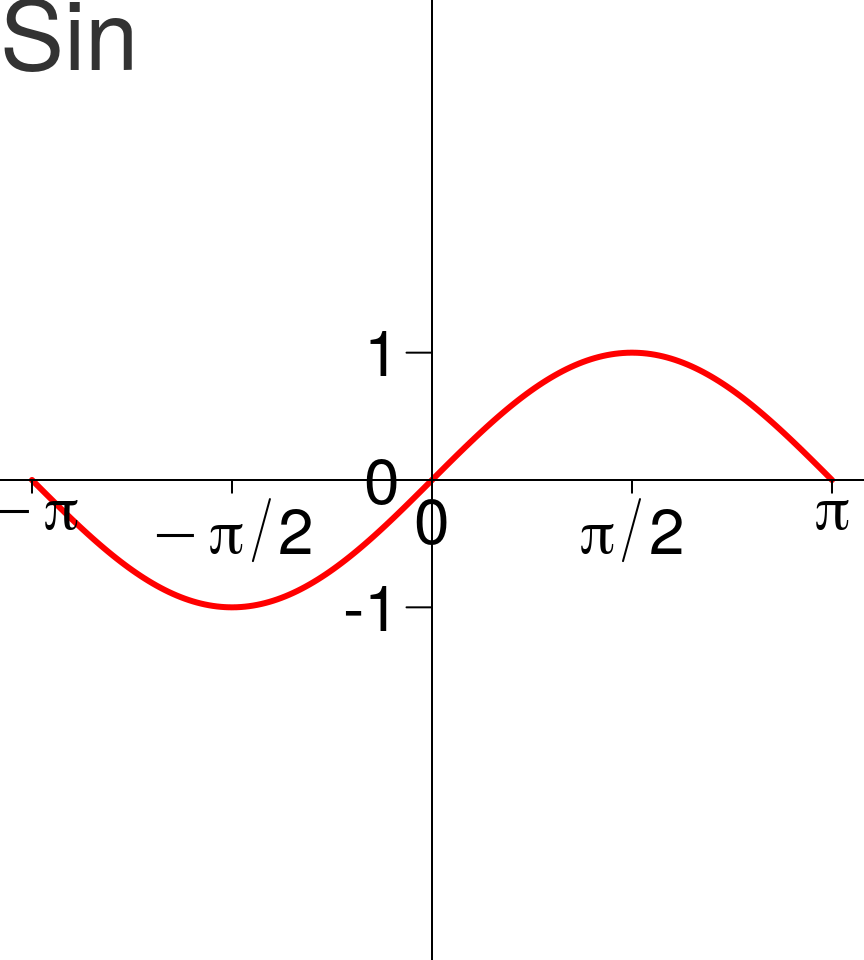
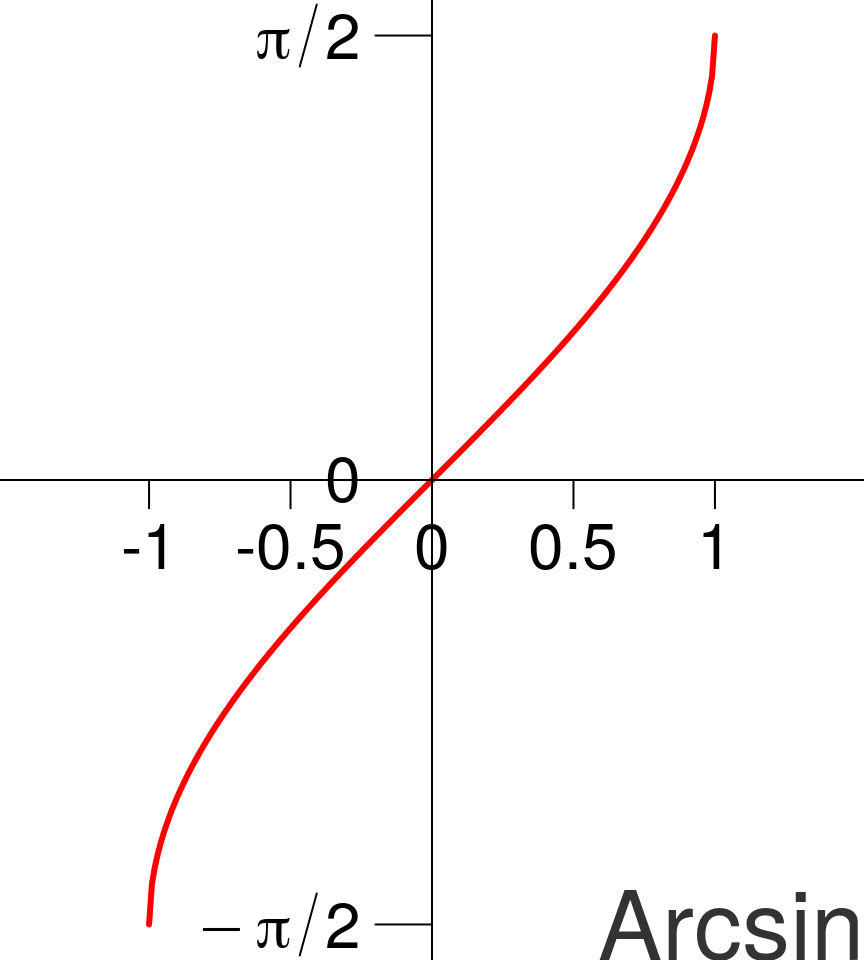
- Pour tout réel \(x \in [-1, 1]\), l’équation d’inconnue \(\theta\) \(\sin(\theta) = x\) admet une unique solution dans \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\). Cette solution est appelée \(\arcsin(x)\).
- Pour tout réel \(x \in \mathbb{R}\), l’équation d’inconnue \(\theta\) \(\tan(\theta) = x\) admet une unique solution dans \(\left]-\frac{\pi}{2}, \frac{\pi}{2}\right[\). Cette solution est appelée \(\arctan(x)\).
Attention à l’intervalle auquel appartient \(\theta\)!!
Cos et Arccos
Sin et Arsin
Tan et Arctan
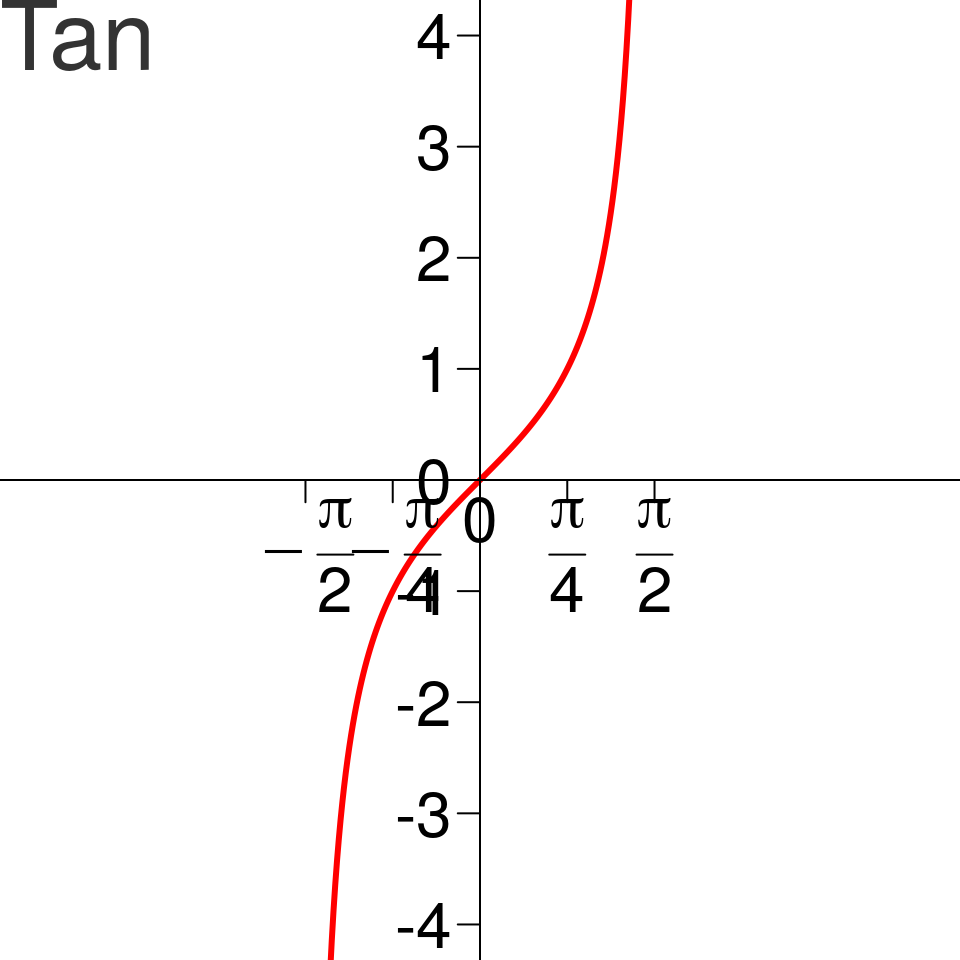
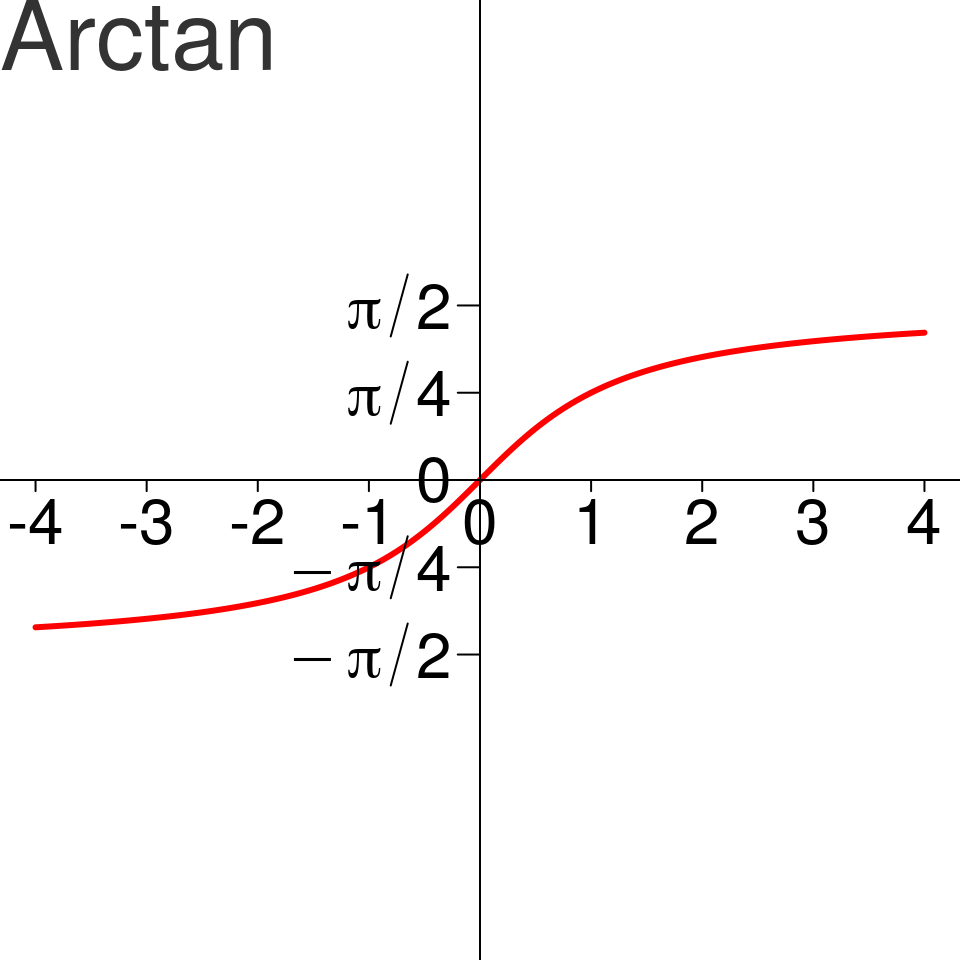
Équations trigonométriques fondamentales (I)
- \(\cos(x)=a\)
- Si \(a \notin [-1, 1]\): pas de solution
- Si \(a \in [-1, 1]\): \(x\) est solution si et seulement si \(\begin{cases} \exists k\in \mathbb{Z} \text{ tel que } x = \arccos(a) + 2k\pi \text{ OU} \\ \exists k\in \mathbb{Z} \text{ tel que } x = -\arccos(a) + 2k\pi\end{cases}\)
- \(\sin(x)=a\)
- Si \(a \notin [-1, 1]\): pas de solution
- Si \(a \in [-1, 1]\): \(x\) est solution si et seulement si \(\begin{cases} \exists k\in \mathbb{Z} \text{ tel que } x = \arcsin(a) + 2k\pi \text{ OU} \\ \exists k\in \mathbb{Z} \text{ tel que } x = \pi -\arcsin(a) + 2k\pi\end{cases}\)
Équations trigonométriques fondamentales (II)
- \(\tan(x)=a\)
\(x\) est solution si et seulement si \(\exists k\in \mathbb{Z}\) tel que \(x = \arctan(a) + k\pi\)
La deuxième formulation est plus générale que la première.
Attention, si on demande les solutions dans un intervalle donnée (par exemple \([0, \pi]\)), il faut sélectionner uniquement les valeurs de \(k\) tel que \(x\) soit dans le bon intervalle. Par exemple, les solutions de \(\sin(x) = 1\) dans \([0, 4\pi]\) sont \(x = \frac{\pi}{2}\) et \(x = \frac{5\pi}{2}\)
Factorisation
Soit \((a, b) \in \mathbb{R}^2\). Il existe \((R, \psi) \in \mathbb{R}^2\) tel que: \[\forall x\in\mathbb{R}, \quad a\cos(x) + b\sin(x) = R\cos(x - \psi)\]
- Si \(a = b = 0\), on peut prendre \(R = \psi = \phi = 0\).
- Sinon, on pose \(R = \sqrt{a^2 + b^2}\). On a alors: \[ a\cos(x) + b\sin(x) = R \left( \frac{a}{R}\cos(x) + \frac{b}{R}\sin(x) \right) \] On remarque que \((a/R)^2 + (b/R)^2 = 1\), il existe donc \(\psi\) tel que \[\cos(\psi) = a/R \text{ et } \sin(\psi) = b/R\] On conclut avec les formules d’addition.
Applications
Résoudre les équations suivantes, dans \(\mathbb{R}\) puis dans \([0, 2\pi]\):
- \(\sin(2x) = \frac{1}{2}\)
- \(\sin(nx) = 0\)
- \(\sin(2x) + \sin(x) = 0\)
- \(\cos(x) + \sin(x) = 1\)
- \(\sqrt{3}\cos(2x) + \sin(2x) > 0\)
Somme et Produit
Notations Somme et Produit
On utilise les signes \(\sum\) et \(\prod\) pour désigner des sommes et des produits
\[ \sum_{i = 0}^n u_i = u_0 + u_1 + \dots + u_{n-1} + u_n\]
\[ \prod_{i = 0}^n u_i = u_0 \times u_1 \times \dots \times u_{n-1} \times u_n\]
L’ensemble des valeurs prises par l’indice \(i\) est ici \(\{0, 1, \dots, n-1, n\}\) mais il peut bien sûr être différent. Par exemple, pour tout \(n \geq 1\), on a \[n! = \prod_{i=1}^n i\].
Variable muette
La variable \(i\) dans la notation précédente est dite muette, elle n’a de sens qu’à l’intérieur de CE symbole \(\sum\) (ou \(\prod\)).
Autrement dit les \(i\) situés à l’extérieur du symbole \(\sum\) sont complétement indépendants des \(i\) situés à l’intérieur du symbole \(\sum\).
On peut donc remplacer le symbole \(i\) par un autre, par exemple \(j\), à condition de rester cohérent: \[ \sum_{i = 0}^n u_i = \sum_{j = 0}^n u_j\]
Exemples
Calculer
- \(\sum_{i=1}^n 1\)
- \(\sum_{i=1}^n i \quad\) (voir exercice de récurrence)
- \(\sum_{i=1}^n n\)
- \(\sum_{i=1}^n (-1)^i\)
- \(\sum_{i=1}^n (-1)^n\)
Linéarité des sommes
Soit \(n\) un entier, \((a_i)_i\) et \((b_i)_i\) deux familles indexées par \(i \in \{1, \dots, n\}\) et \(\lambda\) un réel. On a \[ \begin{align} \sum_{i = 0}^n (a_i + b_i) & = \sum_{i = 0}^n a_i + \sum_{i = 0}^n b_i \\ \sum_{i = 0}^n (\lambda \times a_i) & = \lambda \times \sum_{i = 0}^n a_i \end{align} \]
Décalage d’indices
Soit \((a_i)_i\) une famille indexée par \(\mathbb{N}\). On a pour tout entier \(n\) \[ \sum_{i = 1}^n a_i = \sum_{i = 2}^{n+1} a_{i-1} = \sum_{i = 0}^{n-1} a_{i+1} \]
Ou tout autre décalage du même style, le but étant généralement de se ramener à une somme connue.
Conseil: Posez clairement le changement de variable et faites le en 3 étapes
- Variable Posons \(j = i+1\)
- Bornes Lorsque \(i\) vaut \(1\), \(j\) vaut \(2\) et lorsque \(i\) vaut \(n\), \(j\) vaut \(n+1\).
- Corps de la somme Remplaçons tous les \(i\) par des \(j-1\)
Exemple
En posant \(j = k-1\), montrer que pour tout \(n \in \mathbb{N}\), on a \[\sum_{k=1}^n k^2 = n + 2\sum_{j=1}^{n-1} j + \sum_{j=0}^{n-1} j^2\]
Résultats classique (à connaître)
On peut démontrer tous ces résultats par récurrence.
- \(\sum_{i=1}^n i = \frac{n(n+1)}{2}\)
- \(\sum_{i=1}^n i^2 = \frac{n(n+1)(2n+1)}{6}\)
- \(\sum_{i=1}^n i^3 = \frac{n^2(n+1)^2}{4}\)
Somme des termes d’une suite géométrique
Cette formule sert dans tous les chapitres. Vous la connaissez en général avec \(n = 1\).
Soit \(a \in \mathbb{C}\) et \(n \in \mathbb{N}\), alors \(a^{n+1} - 1 = (a-1)\sum_{i=0}^n a^i\).
On peut la réécrire pour \(a \in \mathbb{C}-\{1\}\) en \[\sum_{i=0}^n a^i = \frac{1 - a^{n+1}}{1-a}\]
Téléscopage
Soit \((u_i)_{i \in \mathbb{N}}\), alors \[\sum_{i=0}^n (u_{i+1} - u_i) = u_{n+1} - u_0\]
Calculer
- \(\sum_{i=1}^n \frac{1}{i(i+1)}\)
- \(\sum_{i=1}^n \ln \left( \frac{i}{i+1} \right)\)
- \(\prod_{i=1}^n \frac{i}{i+1}\)