14 octobre 2019
Introduction
Plan du cours
- Domaine d’étude
- Limites, continuité, dérivabilité et variations
- Comparaison locale de fonction
- Etude locale des fonctions
- Retour sur la limite
Rappel: la notion de dérivée
La dérivée en \(x_0\) d’une fonction \(f\) dépendant de \(x\) est notée \(f'(x_0)\) et définie comme suit \[f'(x_0) = \lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h}\]
-
La dérivée est la limite de deux
petites quantités qui tendent chacune vers \(0\). -
Elle est utilisée (via son
signe ) pour étudier les variations (locales ) de \(f\) et essayer de trouver les optimas (minima et maxima de \(f\)). -
Elle peut être difficile à calculer
rigoureusement
Rappel: le “Formulaire”
Pour éviter de recalculer \(f'\) from scratch à chaque fois, on vous a invité à apprendre par coeur
\[ \begin{align*} \forall \alpha \in \mathbb{R}, \quad (x^{\alpha})' = \alpha x^{\alpha - 1} & &\\ \sin'(x) = \cos(x) & & cos'(x) = -\sin(x) \\ (e^x)' = e^x & & \ln'(x) = \frac{1}{x} \\ (u \times v)' = u'v + uv' & & \left( \frac{u}{v} \right)' = \frac{u'v - uv'}{v^2} \\ (g \circ f)(x) = f'(x) g'(f(x)) & & (f^{-1})'(x) = \frac{1}{f' \circ f^{-1} (x)} \end{align*} \]
À propos du “Formulaire”
- Le formulaire utilise des notations compactes et faciles à retenir mais gêne la compréhension
- On va aussi introduire des notations légèrement plus lourdes (très courantes en physique et en sciences expérimentales) qui mettent en évidence les quantités manipulées.
- Il reste néanmoins nécessaire d’avoir en tête le formulaire lors du calcul “effectif” des dérivées.
Différientielles et dérivées (I)
De façon générale, si deux quantités \(a\) et \(b\) sont liées entre elles par une relation quelconque (algébrique, géométrique, physique, etc), une infime variation de l’une (de \(a\) vers \(a + \text{d}a\)) va entraîner une infime variation de l’autre (de \(b\) vers \(b+\text{d}b\)). \[ \text{Si:} \quad a \to a + \text{d}a \quad \text{alors} \quad b\to b + \text{d}b \]
- La notation \(\text{d}\) dans \(\text{d}a\) et \(\text{d}b\) signale qu’on parle de variations minuscules et même
infinitésimales , c’est à dire aussi petites que l’on veut. - Les physiciens parlent souvent de
différentielle (terme emprunté à Leibniz) pour désigner une variation infinitésimale.
Différentielles et dérivées (II)
- La dérivée peut se concevoir comme le
taux de variation de \(b\) par rapport \(a\), c’est à dire comme le quotient \(\displaystyle \frac{\text{d}b}{\text{d}a}\) dans la limite où les variations \(\text{d}a\) et \(\text{d}b\) sont très petites. - l’idée
principale de la dérivée est la suivanteSi les différentielles sont suffisamment petites, alors elles sont proportionnelles entre elles et le coefficient de multiplication est la dérivée: \[\text{db} = \frac{\text{d}b}{\text{d}a} \text{d}a\]
Différentielles et dérivées (III)
Dans la notation traditionnelle avec \(f'(x)\), on retrouve bien un rapport entre deux variations infinitésimales:
- \(\text{d}f = f(x+h) - f(x)\) (petite variation de \(f\))
- \(\text{d}x = (x+h) - x\) (petite variation de \(x\))
On voit souvent les deux notations
- \(\frac{\text{d}f(x)}{\text{d}x}\) qui insiste sur le rapport entre une petite variation de \(\text{d}f(x)\) et une petite variation de \(\text{d}x\)
- \(\frac{\text{d}}{\text{d}x}f(x)\) qui insiste sur le fait qu’on dérive par rapport à la quantité \(x\).
Les deux sont à connaître.
Différentielles et dérivées (IV)
On considère un angle qui mesure \(\alpha\) radians. Une variation infime de cet angle, notée \(\text{d}\alpha\), entrainera une minuscule variation de \(\sin(\alpha)\), notée \(\text{d}\sin(\alpha)\). Puisque la dérivée de \(\sin\) est \(\cos\), on la relation de proportionalité suivante entre les variations infinitésimales \[
\text{d}\sin(\alpha) = \cos(\alpha) \text{d}\alpha
\] En pratique, la relation précédente est vraie dès que \(\text{d}\alpha\) est
On peut donc adopter une définition, moins rigoureuse mais plus pratique, des différentielles: ce sont des variations
Interprétation graphique (I)
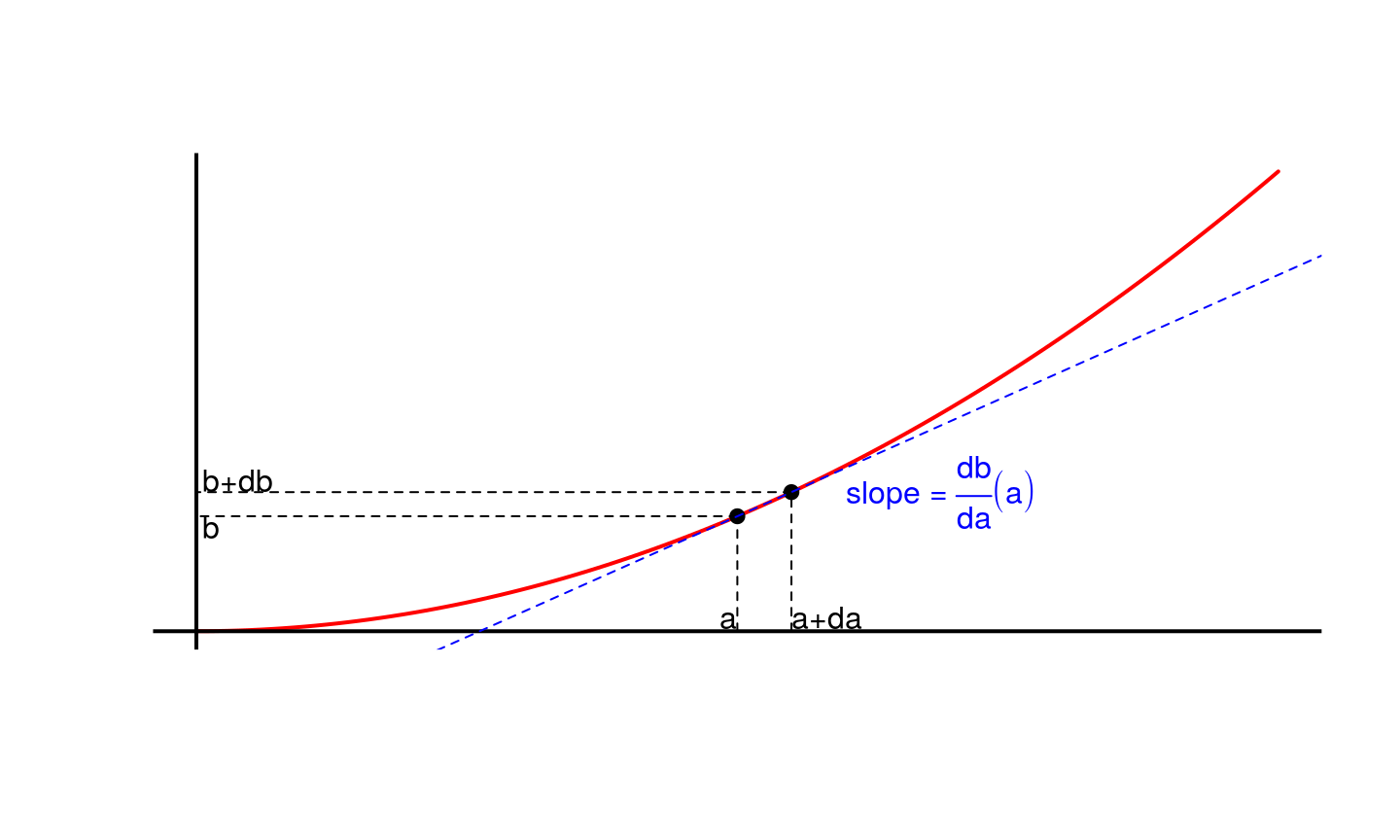
Interprétation graphique (II)
- Le graphique précédent représente \(b(a)\). Localement, entre \((a, b)\) et \((a + \text{d}a, b + \text{d}b)\), la courbe peut-être confondue avec tangente en \((a, b)\) et le coefficient directeur de cette tangente est \(\frac{\text{d}b}{\text{d}a}\).
- Il apparaît clairement sur le graphique précédent, et en toute généralité, que la valeur \(\frac{\text{d}b}{\text{d}a}\)
dépend de \(a\) et qu’il faudrait donc la noter \(\frac{\text{d}b}{\text{d}a}(a)\). - On peut définir la
dérivéé de la dérivée comme \(\text{d}(\frac{\text{d}b}{\text{d}a})/\text{d}a\). Par souci de simplicité, on abrège la notation en \(\frac{\text{d}^2 b}{\text{d}a^2}\) - De même, la dérivée troisième est notée \(\frac{\text{d}^3 b}{\text{d}a^3}\) et plus généralement la dérivée \(n\)-ème est notée \(\frac{\text{d}^n b}{\text{d}a^n}\)
Interprétation graphique (III)
On peut relier les dérivées successives au comportement du graphe de \(b(a)\) au voisinage de \(a\)
- \(b(a)\) indique la
valeur de \(b\) au point \(a\). - La dérivée première \(\frac{\text{d}b}{\text{d}a}(a)\) indique la
pente de la courbe au voisinage de \(a\).- Une pente positive (\(\frac{\text{d}b}{\text{d}a} > 0\)) correspond à une fonction
localement croissante - Une pente négative (\(\frac{\text{d}b}{\text{d}a} < 0\)) correspond à une fonction
localement décroissante - Une pente nulle (\(\frac{\text{d}b}{\text{d}a} = 0\)) correspond à une absence de pente et à une fonction
localement constante
- Une pente positive (\(\frac{\text{d}b}{\text{d}a} > 0\)) correspond à une fonction
Interprétation graphique (IV)
- La dérivée seconde \(\frac{\text{d}^2 b}{\text{d}a^2}(a)\) indique la
concavité de la courbe au voisinage de \(a\).- Une concavité positive (\(\frac{\text{d}^2b}{\text{d}a^2} > 0\)) correspond à une fonction localement
convexe (en forme de creux) en \(a\) - Une concavité négative (\(\frac{\text{d}^2b}{\text{d}a^2} < 0\)) correspond à une fonction localement
concave (en forme de bosse) en \(a\) - Une concavité nulle (\(\frac{\text{d}^2b}{\text{d}a^2} = 0\)) correspond à une absence de courbure et à une fonction localement
linéaire en \(a\)
- Une concavité positive (\(\frac{\text{d}^2b}{\text{d}a^2} > 0\)) correspond à une fonction localement
Interprétation graphique (V)
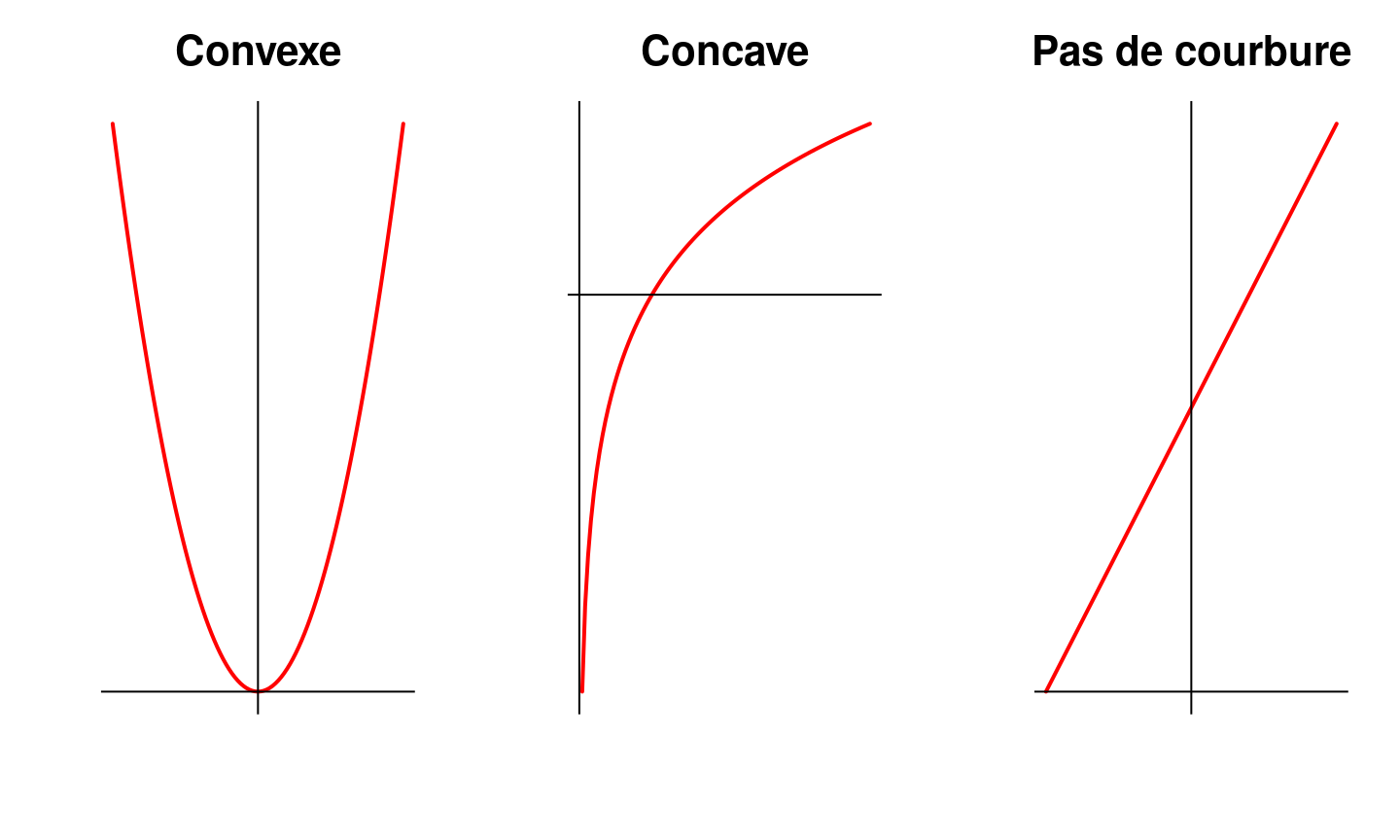
Variable de dérivation
Attention à la
On considère \(b = a^6\) et \(u = a^2\), de sorte que \(b = u^3\). On a \[ \frac{\text{d}b}{\text{d}a}(a) = 6a^5 \quad \text{mais} \quad \frac{\text{d}b}{\text{d}u}(u) = 3u^2 (\neq 6a^5) \]
Dérivée de fonctions composées (I)
Il est très facile de manipuler les différentielles pour retrouver des dérivées compliquées. Il arrive souvent que la variation d’une quantité \(A\) implique la variation d’une quantité \(B\) qui implique la variation d’une quantité \(C\). On a alors des relations de proportionalité entre les différentielles: \[ \text{d}B = \frac{\text{d}B}{\text{d}A} \text{d}A \quad \text{d}C = \frac{\text{d}C}{\text{d}B} \text{d}B \quad \text{d}C = \frac{\text{d}C}{\text{d}A} \text{d}A \] d’où on déduit aisément \[ \frac{\text{d}C}{\text{d}A} = \frac{\text{d}C}{\text{d}B} \times \frac{\text{d}B}{\text{d}A} \]
Dérivée de fonctions composées (II)
En alourdissant un peu les notations pour expliciter les points auquels sont calculés les dérivées, on obtient \[ \frac{\text{d}C}{\text{d}A}(A) = \frac{\text{d}C}{\text{d}B}(B) \times \frac{\text{d}B}{\text{d}A}(A) \]
D’où on tire par analogie (avec \(A=x\), \(B=f(x)\) et \(C=(g\circ f)(x)\) la formule fondamentale du calcul différentiel \[ (g \circ f)'(x) = f'(x) g'(f(x)) \]
On peut évidemment généraliser à la composée de plus de deux fonctions.
Exemple
En posant événtuellement \(u = \omega t + \phi\), calculer la dérivée par rapport à \(t\) de \(\sin(\omega t + \phi)\)
\[ \begin{align*} \frac{\text{d}(\sin(\omega t + \phi))}{\text{d}t}(t) & = \frac{\text{d}\sin(u)}{\text{d}u}(u) \times \frac{\text{d}u}{\text{d}t}(t) \\ & = \cos(u) \times \omega \\ & = \omega \cos(\omega t + \phi) \end{align*} \] On n’oubliera pas de bien tout exprimer en fonction de la variable de dérivation (ici \(t\)).
Lien avec le formulaire
En combinant le mini-formulaire (exception faite de \((f^{-1})'(x)\)) et le résultat précédent, on retrouve des dérivées connues uniquement comme cas particuliers \[ \begin{align*} (e^{u(x)})' = u'(x)e^{u(x)} \\ (\ln(u(x)))' = \frac{u'(x)}{u(x)} \\ (u^\alpha(x))' = \alpha u'(x) u^{\alpha-1}(x)\\ \end{align*} \]
Exercice: Dérivées de fonctions angulaires
Calculer les dérivées suivantes (en décomposant les calculs et en vous servant du formulaire si besoin) \[ \begin{align*} \frac{\text{d}(\tan(\alpha))}{\text{d}\alpha} & & \frac{\text{d}[1/\cos(\alpha)]}{\text{d}\alpha} \\ \frac{\text{d}[1/\sin(\alpha)]}{\text{d}\alpha} & & \frac{\text{d}[1/\tan(\alpha)]}{\text{d}\alpha} \end{align*} \]
Solutions
\[ \begin{align*} \frac{\text{d}(\tan(\alpha))}{\text{d}\alpha} & = \frac{1}{\cos^2(\alpha)} = 1 + \tan^2(\alpha)\\ \frac{\text{d}[1/\cos(\alpha)]}{\text{d}\alpha} & = \frac{\sin(\alpha)}{\cos^2(\alpha)}\\ \frac{\text{d}[1/\sin(\alpha)]}{\text{d}\alpha} & = -\frac{\cos(\alpha)}{\sin^2(\alpha)}\\ \frac{\text{d}[1/\tan(\alpha)]}{\text{d}\alpha} & = \frac{-1}{\sin^2(\alpha)} \end{align*} \]
Exercices (dérivées de fonctions de bases)
\[ \begin{align*} \frac{\text{d}[u\ln(u) - u ]}{\text{d}u} & & \frac{\text{d}[(v - 1)e^v]}{\text{d}v}\\ \frac{\text{d}[1/(1+\epsilon^2)]}{\text{d}\epsilon} & & \frac{\text{d}[1/\tan{\alpha}]}{\text{d}\alpha} \\ \frac{\text{d}^2[\sin^2(\theta)]}{\text{d}\theta^2} & & \frac{\text{d}^2[x\sqrt{x}]}{\text{d}x^2} \\ \frac{\text{d}^2[\ln(y)]}{\text{d}y^2} & & \frac{\text{d}^2[z^3+3z^2+3z+1]}{\text{d}z^2} \end{align*} \]
Solutions
Calculer les dérivées suivantes (en décomposant les calculs et en vous servant du formulaire si besoin) \[ \small \begin{align*} \frac{\text{d}[u\ln(u) - u ]}{\text{d}u} = \ln(u) & & \frac{\text{d}[(v - 1)e^v]}{\text{d}v} = ve^v \\ \frac{\text{d}[1/(1+\epsilon^2)]}{\text{d}\epsilon} = \frac{-2\varepsilon}{(1+\varepsilon^2)^2}& & \frac{\text{d}[1/\tan{\alpha}]}{\text{d}\alpha} = \frac{-1}{\sin^2(\alpha)} \\ \frac{\text{d}^2[\sin^2(\theta)]}{\text{d}\theta^2} = 2\cos(2\theta) & & \frac{\text{d}^2[x\sqrt{x}]}{\text{d}x^2} = \frac{3}{4\sqrt{x}}\\ \frac{\text{d}^2[\ln(y)]}{\text{d}y^2} = \frac{-1}{y^2} & & \frac{\text{d}^2[z^3+3z^2+3z+1]}{\text{d}z^2} = 6z + 6 \end{align*} \]
Exercices (dérivées de fonctions composées)
Calculer les dérivées suivantes (en décomposant les calculs et en vous servant du formulaire si besoin) \[ \begin{align*} \frac{\text{d}[(1+u^3)^4]}{\text{d}u} & & \frac{\text{d}[\sqrt{1+v^2}]}{\text{d}v} \\ \frac{\text{d}[\ln(1-x)]}{\text{d}x} & & \frac{\text{d}[2\sin(\alpha - \frac{\pi}{8})]}{\text{d}\alpha} \\ \frac{\text{d}[\tan^2(\theta)]}{\text{d}\theta} & & \frac{\text{d}[e^{-y^2}]}{\text{d}y} \\ \frac{\text{d}[1/\sqrt{1+u^2}]}{\text{d}u} & & \frac{\text{d}[\sqrt{z^3 + 3z^2 + 3z + 1}]}{\text{d}z} \end{align*} \]
Solutions
Calculer les dérivées suivantes (en décomposant les calculs et en vous servant du formulaire si besoin) \[ \scriptsize \begin{align*} \frac{\text{d}[(1+u^3)^4]}{\text{d}u} = 12u^2(1+u^3)^3 & & \frac{\text{d}[\sqrt{1+v^2}]}{\text{d}v} = \frac{v}{\sqrt{1+v^2}} \\ \frac{\text{d}[\ln(1-x)]}{\text{d}x} = \frac{-1}{1 - x} & & \frac{\text{d}[2\sin(\alpha - \frac{\pi}{8})]}{\text{d}\alpha} = 2\cos\left(\alpha - \frac{\pi}{8}\right)\\ \frac{\text{d}[\tan^2(\theta)]}{\text{d}\theta} = 2\tan(\theta) + 2\tan^3(\theta))& & \frac{\text{d}[e^{-y^2}]}{\text{d}y} = -2y e^{-y^2}\\ \frac{\text{d}[1/\sqrt{1+u^2}]}{\text{d}u} = -\frac{u}{(1+u^2)^{3/2}} & & \\ \end{align*} \] \[ \scriptsize \frac{\text{d}[\sqrt{z^3 + 3z^2 + 3z + 1}]}{\text{d}z} = \frac{3z^2 + 6z + 3}{2\sqrt{z^3 + 3z^2 + 3z + 1}} \]
Dérivées de fonctions réciproques
Les fonctions réciproques jouent un rôle fondamentales en sciences expérimentales. Il est souvent possible d’
- \(a\) en fonction de \(b\) (\(a = a(b)\))
- \(b\) en fonction de \(a\) (\(b = b(a)\))
C’est le cas si \(a(b)\) (ou \(b(a)\)) est une
Dans le formalisme mathématique, on note plutôt \(y = f(x)\) et \(x = f^{-1}(y)\).
Graphes de fonctions réciproques
Les graphes de fonctions réciproques s’obtiennent aisément en
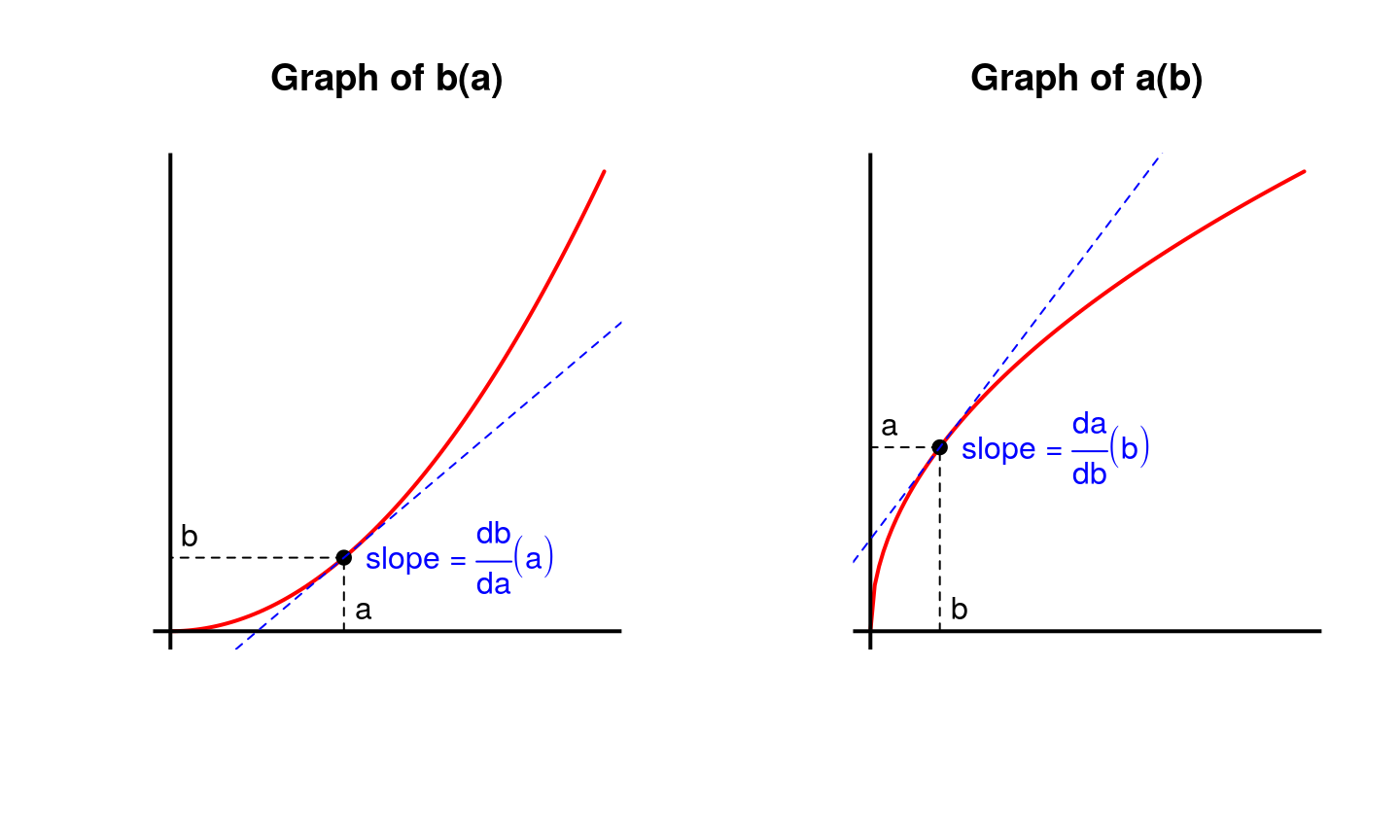
Dérivées de fonctions réciproques (II)
Au vu des relations de proportionalités entre les différentielles: \[ \text{db} = \frac{\text{d}b}{\text{d}a} \text{d}a \qquad \text{da} = \frac{\text{d}a}{\text{d}b} \text{d}b \] On a évidemment la relation suivante: \[ \frac{\text{d}b}{\text{d}a}(a) = \left( \frac{\text{d}a}{\text{d}b}(b) \right)^{-1} \]
Dérivées de fonctions réciproques (III)
Attention à bien calculer les dérivées au point d’intérêt.
Par exemple, si \(a\) et \(b\) sont des quantités positives, alors \(b=\sqrt{a} \Leftrightarrow a = b^2\).
Sachant que \(\frac{\text{d}a}{\text{d}b} = \frac{\text{d}(b^2)}{\text{d}b} = 2b\), on déduit tout de suite que \(\frac{\text{d}b}{\text{d}a} = \frac{1}{2b}\). Mais pour que ce résultat soit intéressant, il faut le
D’un point de formel, on retrouve la formule de la dérivée de la fonction réciproque. Si \(y = f(x)\) et \(x = f^{-1}(y)\), on a \[ (f^{-1})'(y) = \frac{\text{d}x}{\text{d}y}(y) = \left( \frac{\text{d}y}{\text{d}x}(x) \right)^{-1} = \frac{1}{f'(x)} = \frac{1}{f'\circ f^{-1}(y)} \]
Exercice: Dérivées de fonctions trigonométriques réciproques
Les fonctions \(\arcsin(x)\), \(\arccos(x)\) et \(\arctan(x)\) sont les réciproques (sur un certain intervalle) des fonctions trigonométriques \(\sin(x)\), \(\cos(x)\), \(\tan(x)\).
Montrer que (les résultats sont à connaître)
- \(\frac{\text{d}\arcsin(x)}{\text{d}x} = \frac{1}{\sqrt{1 - x^2}}\)
- \(\frac{\text{d}\arccos(x)}{\text{d}x} = \frac{-1}{\sqrt{1 - x^2}}\)
- \(\frac{\text{d}\arctan(x)}{\text{d}x} = \frac{1}{1+x^2}\)
Indice: Quand \(\cos(x) >0\), on a \(\cos(x) = \sqrt{1 - \sin^2(x)}\). Pareil pour \(\sin(x)\).
Application des dérivées
Théorème et inégalité des acroissements finis (TAF/IAF)
Soit \(f: I = [a,b] \to \mathbb{R}\) une fonction dérivable sur \(I\). Il existe alors au moins un point \(c\) dans l’intervalle \((a, b)\) tel que \[f(b) - f(a) = f'(c) (b - a)\]
Soit \(f: I = [a,b] \to \mathbb{R}\) une fonction dérivable sur \(I\). On suppose que pour tout \(x \in (a, b)\), on a \(m \leq f'(x) \leq M\). Alors, pour tout \(x \in (a, b)\), \[m(x - a) \leq f(x) - f(a) \leq M(x-a)\]
TAF et IAF (II)
- TAF: La corde \([AB]\) entre \(A = (a, f(a))\) et \(B = (b, f(b))\) est parallèle à une des tangentes à la courbe (TAF).
- IAF: Si les tangentes extrêmes ont pour pentes \(m\) et \(M\), la courbe est comprise entre \(a\) et \(b\) entre les droites passant par \(A\) et de coefficient directeur \(m\) et \(M\).
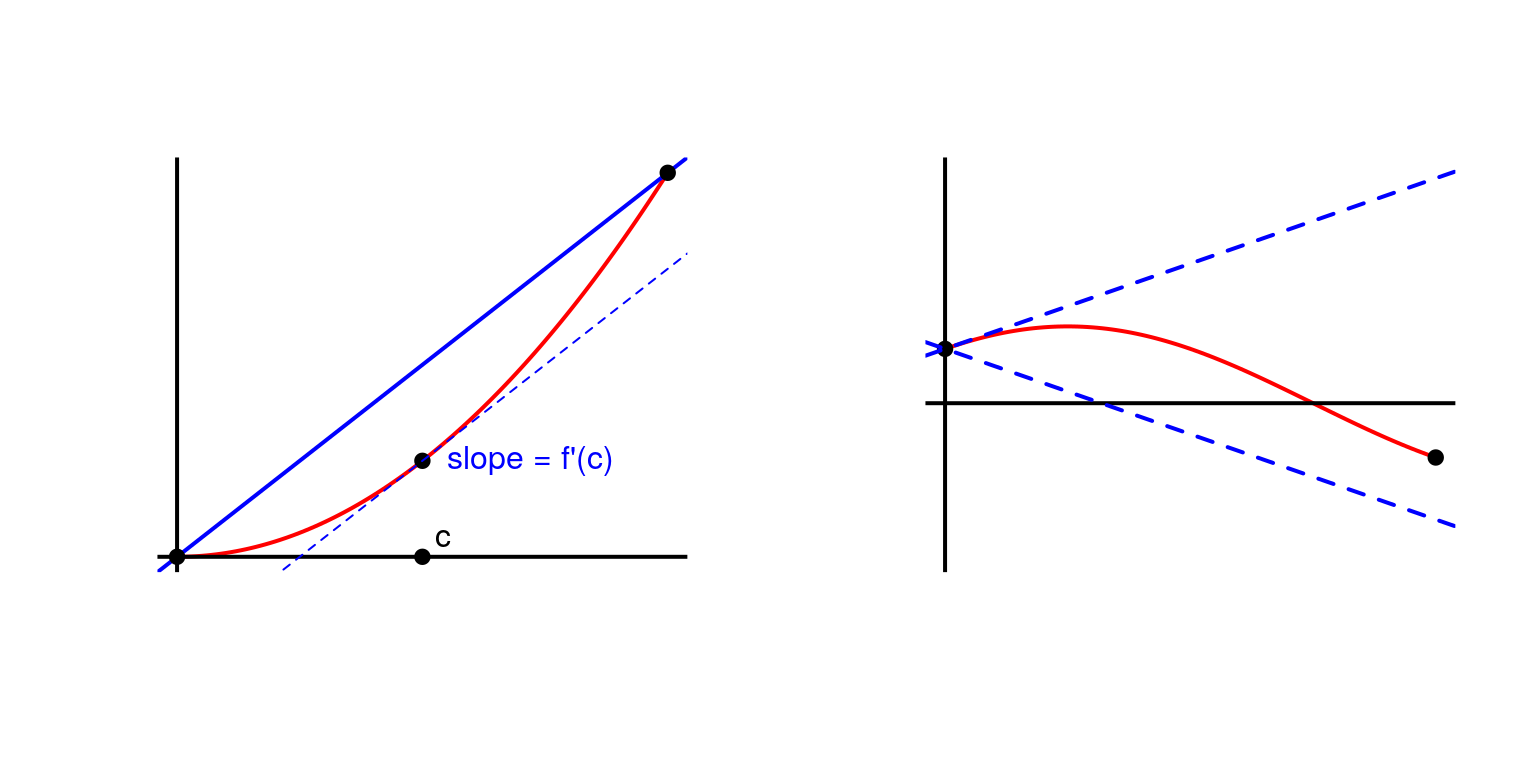
Tableau de variations
Soit \(f: I = [a,b] \to \mathbb{R}\) une fonction continue sur \(I\) et dérivable sur \(I\) (sauf éventuellement en un nombre
- \(f' \geq 0\) (resp. \(f > 0\) sauf éventuellement en un nombre
fini de points) sur \(I\), alors \(f\) est croissante (resp. strictement croissante) sur \(I\) - \(f' \leq 0\) (resp. \(f < 0\) sauf éventuellement en un nombre
fini de points) sur \(I\), alors \(f\) est décroissante (resp. strictement décroissante) sur \(I\) - \(f' = 0\) sur \(I\), alors \(f\) est constante sur \(I\)
C’est une conséquence directe du TAF.
Théorème de la bijection
Soit \(f\) une fonction
De plus \(f(I)\) se déduit simplement de \(I\) et de la monotonie de \(f\) comme suit: \[ \begin{array}{|c||c|c|} \hline \text{forme de } I & f \text{ croissante} & f \text{ décroissante} \\ \hline \hline [a, b] & f(I) = [f(a), f(b)] & f(I) = [f(b), f(a)] \\ \hline [a, b) & f(I) = [f(a), \lim_{b^-} f) & f(I) = (\lim_{b^-} f , f(a)] \\ \hline (a, b] & f(I) = (\lim_{a^+} f, f(b)] & f(I) = [f(b) , \lim_{a^+} f) \\ \hline (a, b) & f(I) = (\lim_{a^+} f, \lim_{b^-} f) & f(I) = (\lim_{b^-} f , \lim_{a^+} f) \\ \hline \end{array} \]
On utilise souvent le signe de la dérivée pour prouver la stricte monotonie
Exercices (I)
Déterminer l’image de l’intervalle \(I\) par les fonctions suivantes: \[ \small \begin{align} f: x \mapsto e^x - x & & \text{pour } I = \mathbb{R} & & \text{pour } I = (0, e) \\ g: x \mapsto \ln(x+1) -x & & \text{pour } I = (-1, 0) & & \text{pour } I = [0, e] \\ h: x \mapsto \frac{e^x + 1}{x+2} & & \text{pour } I = (-\infty, -2) & & \text{pour } I = \mathbb{R}_+ \\ \end{align} \]
Solutions
- \(f\) est strictement décroissante sur \(\mathbb{R}_-\), strictement croissante sur \(\mathbb{R}_+\). De plus, \(\lim_{-\infty} f = \lim_{+\infty} f = +\infty\) et \(f(0) = 1\) donc \(f(\mathbb{R}) = [1, +\infty)\) et \(f((0, e)) = (1, e^e - e)\).
- \(g\) est strictement croissante sur \((-1, 0]\) et strictement décroissante sur \([0, +\infty)\). De plus, \(\lim_{-1} f = -\infty\), \(f(0) = 0\) et \(f(e) = \ln(1+e) - e\) donc \(f((-1, 0)) = (-\infty, 0)\) et \(f([0, e]) = [\ln(1+e) - e, 0]\)
- \(h\) est strictement décroissante sur \((-\infty, -2)\) et strictement croissante sur \([0, +\infty)\). De plus, \(\lim_{-\infty} f = 0\), \(\lim_{-2} f = -\infty\), \(f(0) = 1\) et \(\lim_{+\infty} f = +\infty\) donc \(f((-\infty, -2)) = (-\infty, 0)\) et \(f([0, \infty)) = [1, +\infty)\)
Exercices (II)
- En fonction de la valeur du paramètre \(m\), indiquer le nombre de solutions de l’équation \(x^3 - x = m\).
- Montrer que l’équation \(x^3 + x + 1 = 0\) admet une unique solution (notée \(\alpha\)) et que \(-1 < \alpha < 0\).
Solutions
Corrigé en cours
Application (I)
Trouver toutes les applications dérivables de \(\mathbb{R}_+^*\) telles que \(f(xy) = f(x) + f(y)\) (on peut se rappeler que \(\ln(x)\) est une primitive de \(1/x\))
On raisonne par analyse-synthèse.
Application (II)
Analyse Soit \(f\) une telle fonction. Soit \(y > 0\), on pose \(g_y: x \mapsto f(xy)\). En dérivant \(g_y\), on obtient: \[ g'_y(x) = y f'(xy) = f'(x) \] Et en particulier, en \(x = 1\), \(f'(y) = f'(1) / y\) d’où on déduit que \(f(y) = a (\ln(y) + C)\) avec \(a = f'(1)\) et \(C\) une constante à déterminer. On a également \(f(1) = f(1 \times 1) = 2f(1)\) donc \(f(1) = 0\) et \(aC = 0\), \(a = 0\) ou \(C = 0\). Au final \(f\) doit être de la forme \(f(y) = a\ln(y)\).
Synthèse Soit \(f\) une fonction de la forme \(f(y) = a \ln(y)\) avec \(a \in \mathbb{R}\). On vérifie aisément que \(f\) est dérivable et satisfait \(f(xy) = f(x) + f(y)\) sur \(\mathbb{R}_+^*\)
Dérivées successives
On définit les dérivées successives de \(f\) en un point \(a \in D_f\) (resp. sur \(I \subset D_f\)) par \[ \begin{cases} & f^{(0)} & = & f \\ \forall k \in \mathbb{N}^* & f^{(k)} & = & [f^{(k-1)}]' \end{cases} \]
- On dit que \(f\) est \(k\) fois dérivable en \(a\) (resp. sur \(I\)) lorsque \(f^{(k)}(a)\) existe (resp. \(f^{(k)}\) est définie sur \(I\)).
- On dit que \(f\) est infiniment dérivable en \(a\) (resp. sur \(I\)) lorsque \(f^{(k)}(a)\) existe (resp. \(f^{(k)}\) est définie sur \(I\)) pour tout \(k \in \mathbb{N}\).
Dérivées successives (II)
- Une fonction \(f\) est dite \(D^k\) (en \(a\), sur \(I\)) si elle est \(k\)-fois dérivable (en \(a\), sur \(I\))
- Une fonction \(f\) est dite \(C^k\) (en \(a\), sur \(I\)) si elle est \(k\)-fois dérivable et que \(f^{(k)}\) est continue (en \(a\), sur \(I\)).
- Une fonction \(f\) est dite \(C^\infty\) (en \(a\), sur \(I\)) si elle est infiniment dérivable (en \(a\), sur \(I\)) (et on a \(D^\infty = C^\infty\))
Exemples
- Tout polynôme est infiniment dérivable sur \(\mathbb{R}\)
- Toute fraction rationnelle est infiniment dérivable sur son domaine de définition
- \(x \mapsto \sqrt{x}\) est infiniment dérivable sur \(\mathbb{R}_+^*\) mais seulement \(C^0\) en \(0\).
- \(\sin\), \(\cos\), \(\tan\), \(\exp\), \(\ln\) sont \(C^\infty\) sur leurs domaines respectifs
Exercices
Etudier l’existence des dérivées successives de
- \(f: x \mapsto (x - 1)^{3/2}\)
- \(g: x \mapsto \begin{cases} x^2 & \text{si} & x \geq 0 \\ x^3 & \text{si} & x < 0 \end{cases}\)
- \(h: x \mapsto \begin{cases} x^2 \sin(1/x) & \text{si} & x \neq 0 \\ 0 & \text{si} & x = 0 \end{cases}\)
Solutions
- \(f\) est définie sur \([1, +\infty)\), \(C^{\infty}\) sur \((1, +\infty)\) mais seulement \(C^1\) (dérivable de dérivée continue) en \(1\).
- \(g\) est \(C^\infty\) sur \(\mathbb{R}^*\) mais seulement \(C^1\) en \(0\).
- \(h\) est \(C^\infty\) sur \(\mathbb{R}^*\) mais seulement \(C^1\) en \(0\).
Étude de fonctions
Tangentes verticales
Soit \(f: I = [a,b] \to \mathbb{R}\) une fonction continue sur \(I\), dérivable sur \(I\setminus \{a\}\). Si \(\lim_{a+} f' = \pm \infty\), alors le graphe \(f\) admet une tangente verticale en \(a\).
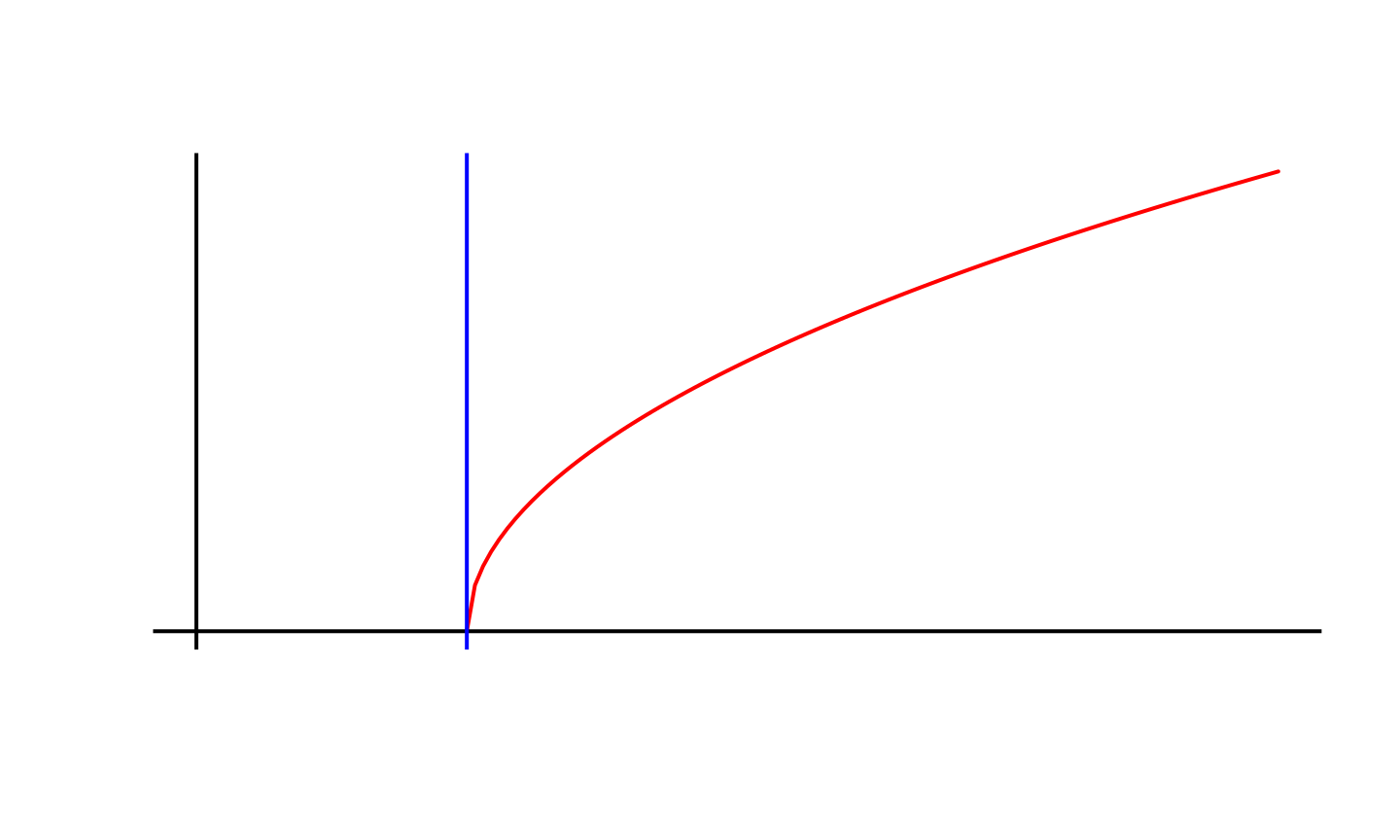
Recherche de minimums
Soit \(f: I \to \mathbb{R}\) une fonction dérivable qu’on cherche à minimiser (typiquement une énergie, un temps, une surface). Il est parfois plus facile de chercher le minimum de \(f\) en passant par \(f'\) qu’en faisant le tableau de variation complet de \(f\).
Les points critiques de \(f\) sont les points d’annulation de \(f'\)
Les minimums
Il suffit donc d’étudier les points critiques (généralement peu nombreux) pour savoir où \(f\) est (localement) minimum et de comparer ces mininums pour trouver le minimum global.
On note aussi que maximiser \(f\) revient à minimiser \(-f\), on se contente donc ici de chercher des minimums.
Point critique et minimum
Attention, un minimum est toujours un point critique mais un point critique n’est pas forcément un minimum.
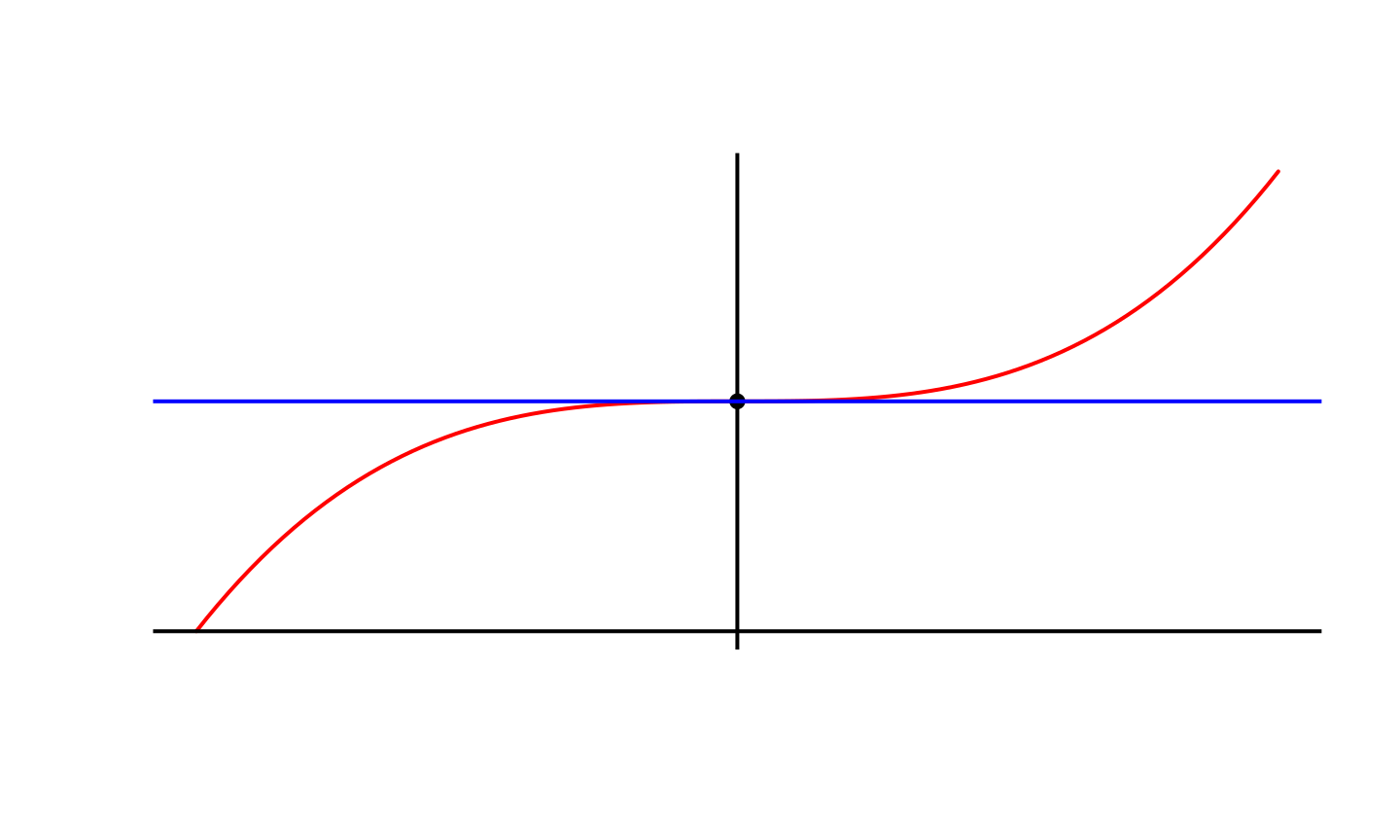
Nature des points critiques
Si \(f\) est deux-fois dérivable, on peut déterminer si un point critique (hors bornes du domaine) est un maximum local ou un minimum local en fonction du signe de \(f''\).
Soit \(f: I = [a,b] \to \mathbb{R}\) une fonction deux fois dérivable sur \(I\) et \(a\) un point d’annulation de \(f'\).
- \(f''(a) > 0\), \(a\) est un minimum local de \(f\)
- \(f''(a) < 0\), \(a\) est un maximum local de \(f\)
- \(f''(a) = 0\) on peut pas conclure.
Nature du point quand \(f''(a) \neq 0\)
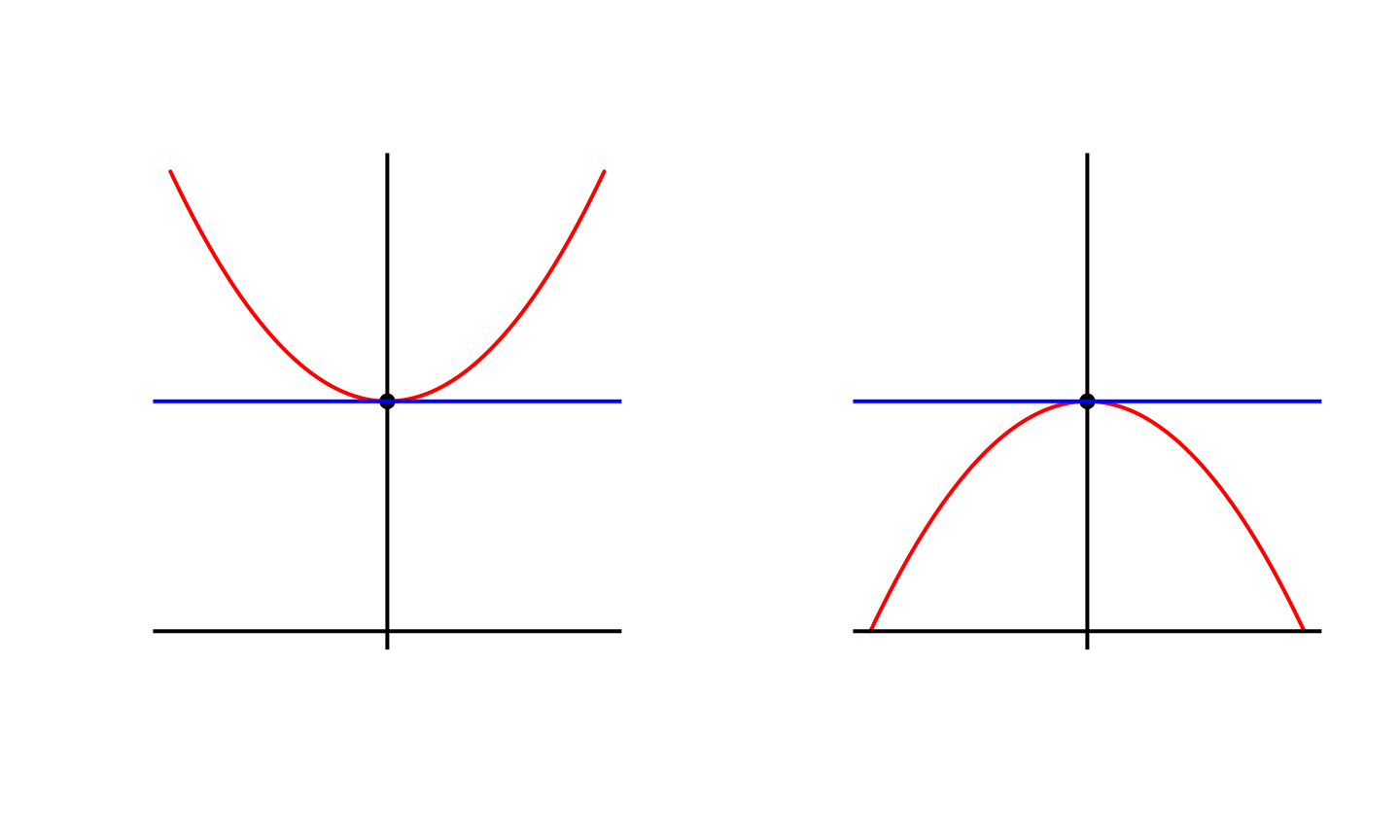
Nature du point quand \(f''(a) = 0\)
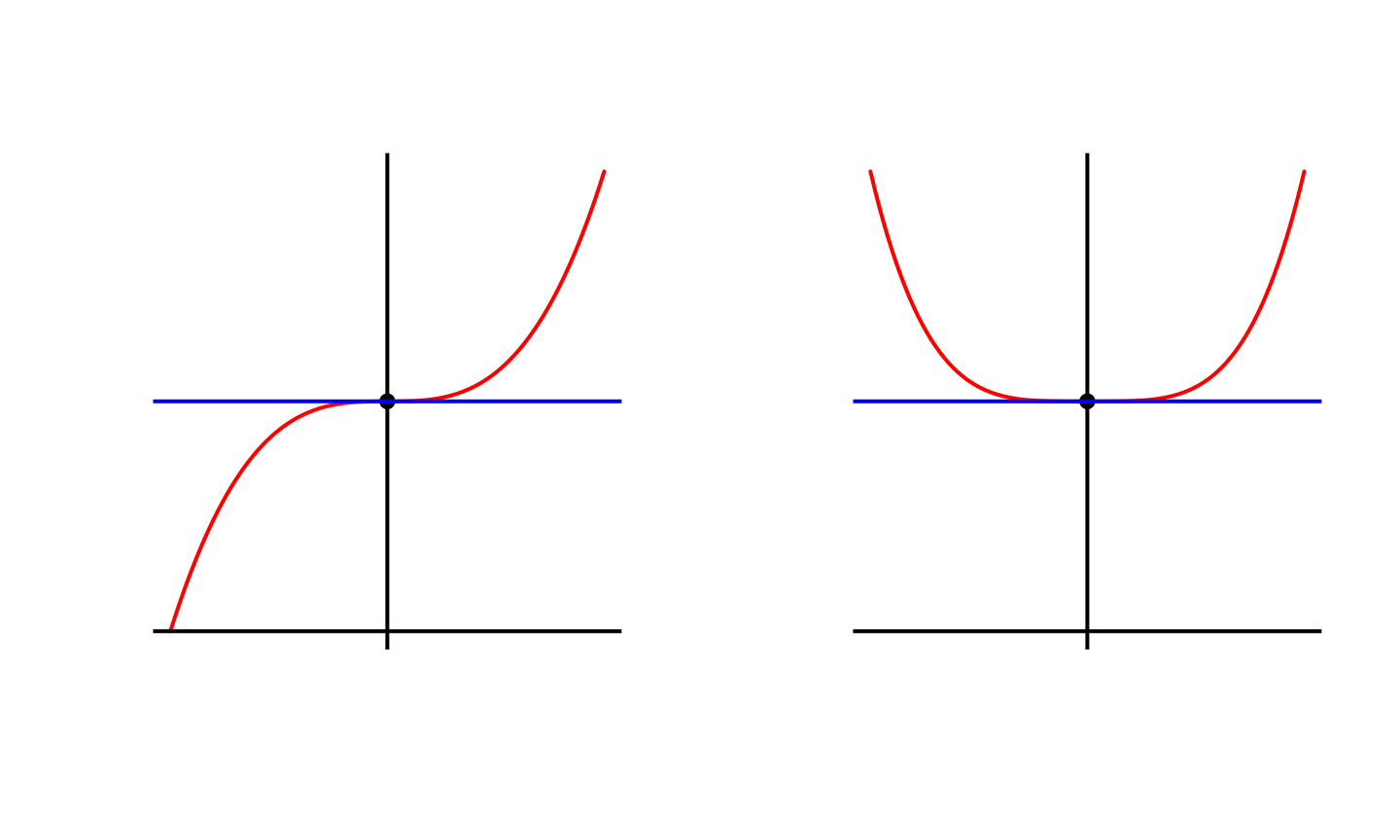
Mise en oeuvre
Application (I)
Un pièton peut s’éloigner de \(x\) mètres d’une antenne-relais (située en \(x=0\)). La puissance \(f(x)\) des ondes-relais reçues est donnée par \[f(x) = \frac{e^{-(x - \alpha)^2}}{x}\] avec \(\alpha = 2\).
- À quelle distance doit-il se placer pour recevoir le moins d’ondes-relais?
- Même question s’il ne peut s’éloigner de plus de 3 mètres?
- Où doit-il se placer pour maximiser la réception?
- Même question s’il ne peut pas s’approcher de l’antenne à moins de 1 mètre.
Application (II)
Un campeur est situé à \(3\) kilomètres en aval de sa tente, de l’autre côté d’une rivière qui fait \(1\) km de large. Il nage à \(2\) km/h et marche à \(4\) km/h.
- Quel est le chemin le plus rapide pour rentrer?
- Même question s’il existe un pont en face de sa tente.
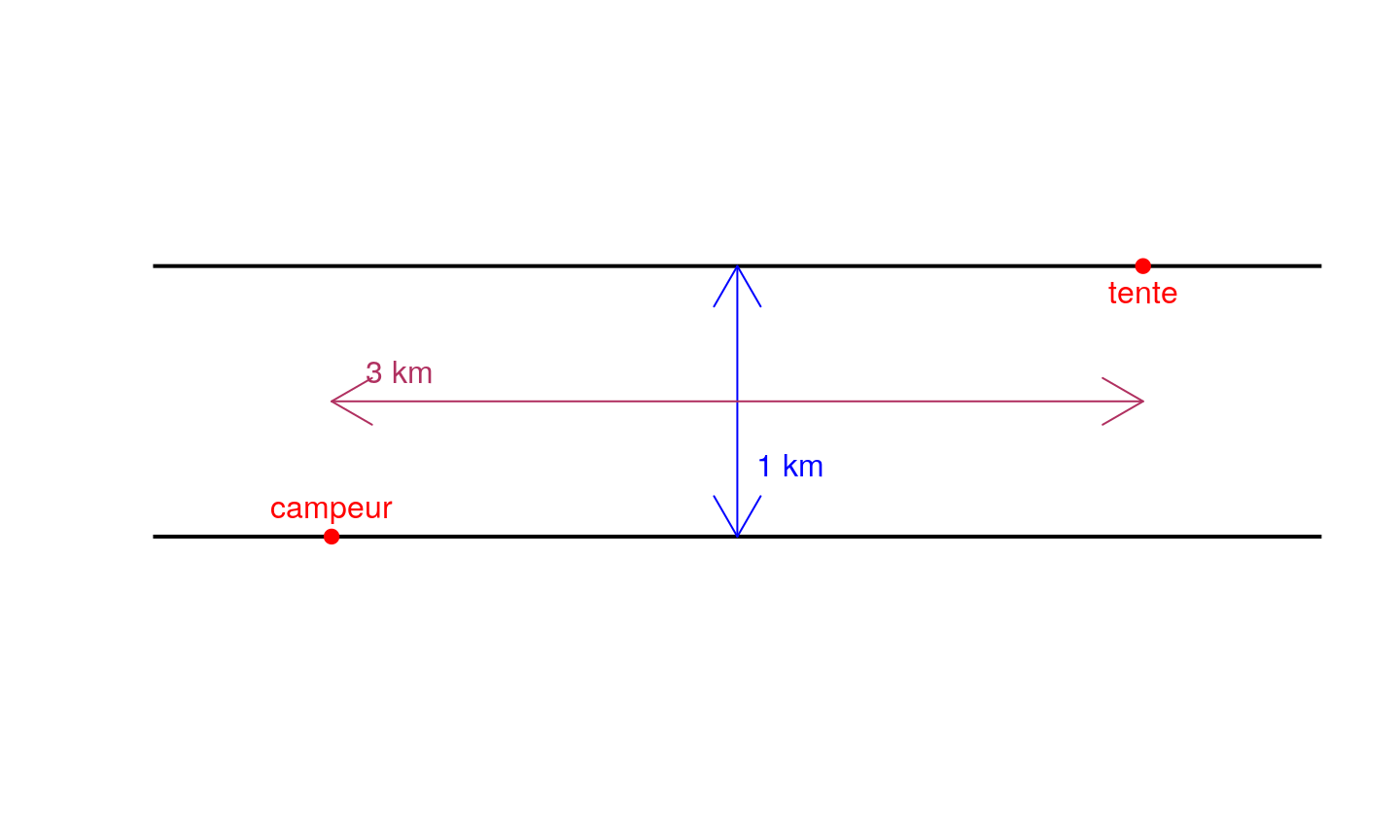
Correction
On note \(3 - x\) la distance entre la position initiale du campeur et le point où il entre dans la rivière et se met à nager pour rejoindre sa tente.
Pour minimiser son trajet, le campeur marche en ligne droite jusqu’au point de traversée, marchant \(3 - x\) km, puis nage en ligne droite du point de traversée jusqu’à la tente, nageant \(\sqrt{1 + x^2}\) km (d’après le théorème de Pythagore). 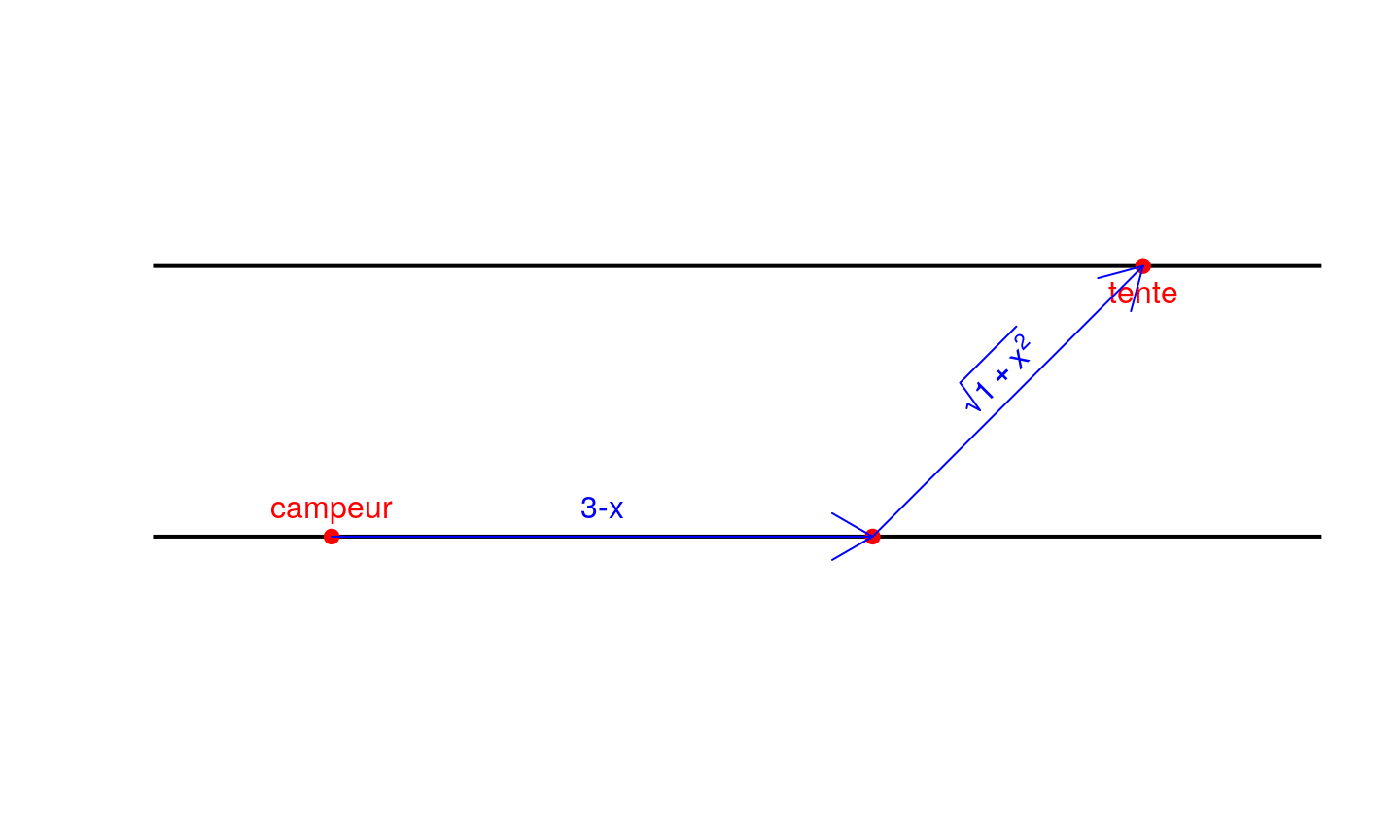
Correction (II)
Son temps total de parcours \(T(x)\) est donc donné par \[ T(x) = \frac{3-x}{4} + \frac{\sqrt{1+x^2}}{2} \] avec \(x \in [0, 3]\). \(T\) est dérivable sur \([0, 3]\) (comme somme et composée de fonctions dérivables) et a pour dérivée: \(T'(x) = -\frac{1}{4} + \frac{x}{2\sqrt{1 + x^2}}\). On cherche le point d’annulation de \(T'\).
\[ T'(x) = 0 \Leftrightarrow 4x = \sqrt{1 + x^2} \Leftrightarrow 16x^2 = 1 + x^2 \Leftrightarrow x = \pm 1/\sqrt{15}\] Les points critiques de \(T\) dans \([0, 3]\) sont donc \(\{0, 1/\sqrt{15}, 3\}\). En évaluant \(T\) en chacun des points, on trouve \(T(0) = 1.25\), \(T(3) = \sqrt{10}/2 \simeq 1.58\) et \(T(1/\sqrt{15}) \simeq 1.20\). Le minimum sur \([0, 3]\) est donc atteint en \(x = 1/\sqrt{15}\) et le trajet le plus rapide consiste à marcher \(3 - 1/\sqrt{15}\) km le long de la rive avant de nager en ligne droite vers la tente.
Correction (III)
S’il y a un pont en face de la tente, une autre stratégie consiste à marcher jusqu’au pont puis à le traverser à pied (plutôt qu’à la nage). On a alors \(T(0) = 1 < T(1/\sqrt{15})\) et le chemin le plus rapide consiste alors à marcher jusqu’au pont pour traverser la rivière à pied sur le pont.
Exercices (I)
Trouver les minimums et maximums globaux des fonctions suivantes (il est recommandé de s’aider d’un ordinateur pour calculer \(f\) en différentes valeurs, les exercices avec un (*) sont difficiles): \[ \begin{align*} f(z) = 2z^4 - 16z^3 + 20z^2 - 7 & & \text{ pour } z \in [-2, 6] \\ f(z) = 2z^4 - 16z^3 + 20z^2 - 7 & & \text{ pour } z \in [-2, 4] \\ f(z) = 2z^4 - 16z^3 + 20z^2 - 7 & & \text{ pour } z \in [0, 2] \\ f(t) = \frac{3 - 4t}{t^2 + 1} & & \text{ pour } t \in [-2, 4] \\ f(x) = 3\cos(2x) - 5x & & \text{ pour } x \in [0, 6] \quad (*)\\ f(x) = x\cos(x) - \sin(x) & & \text{ pour } x \in [-15, -5] \\ f(z) = z^2e^{1-z} & & \text{ pour } z \in [-1/2, 5/2]\\ f(t) = \ln(t^2 + t + 3) & & \text{ pour } t \in [-2, 2] \end{align*} \]
Solutions
\[ \small \begin{array}{|cccc|} \hline f & I & \min & \max \\ \hline \hline 2z^4 - 16z^3 + 20z^2 - 7 & [-2, 6] & -257 & 233 \\ 2z^4 - 16z^3 + 20z^2 - 7 & [-2, 4] & -199 & 233 \\ 2z^4 - 16z^3 + 20z^2 - 7 & [0, 2] & -23 & -1 \\ \frac{3-4t}{t^2 + 1} & [-2, 4] & f(1 + \sqrt{2}) & f(1 - \sqrt{2}) \\ 3\cos(2x) - 5x & [0, 6] & f(0) & f(30) \\ x\cos(x) - \sin(x) & [-15, -5] & f(-5) & f(-15) \\ x^2e^{1 - x} & [-1/2, 5/2] & f(0) = 0 & f(2) = 4/e & \\ \ln(t^2 + t + 3) & [-2, 2] & \ln(3.75) & 2\ln(3) \\ \hline \end{array} \]
Exercices (II)
Calculer, à l’aide de dérivées, les limites suivantes: \[ \begin{align*} \lim_{x \to 3} \frac{\ln(x) - \ln(3)}{x - 3} & & \lim_{x \to 2} \frac{\sqrt{x+2} - 2}{x - 2} \\ \lim_{x \to 1} \frac{e^x - e}{x - 1} & & \lim_{x \to -1} \frac{x^{2017} + 1}{x + 1} \end{align*} \]
Solutions
\[ \begin{align*} \lim_{x \to 3} \frac{\ln(x) - \ln(3)}{x - 3} = \frac{1}{3} & & \lim_{x \to 2} \frac{\sqrt{x+2} - 2}{x - 2} = \frac{1}{4}\\ \lim_{x \to 1} \frac{e^x - e}{x - 1} = e & & \lim_{x \to -1} \frac{x^{2017} + 1}{x + 1} = 2017 \end{align*} \]
Exercices (III)
À l’aide de la méthode de votre choix, montrez les inégalités (dites de convexité) suivantes: \[ \small \begin{align*} \forall x \in \mathbb{R} & \quad e^x \geq 1 + x \\ \forall x \geq 0 & \quad xe^x + 1 \geq e^x \geq 1 + x + \frac{x^2}{2} \\ \forall x \in (-1, +\infty) & \quad \ln(1+x) \leq x \\ \forall x \leq 0 & \quad 1+x \leq e^x \leq 1 + x + \frac{x^2}{2} \end{align*} \]
Exercices (IV)
On considère la fonction \(f(x) = (x+1)e^{-x}\)
- Montrer par récurrence que pour tout entier \(n \geq 0\), il existe deux réels \(a_n\) et \(b_n\) tels que \(f^{(n)}(x) = (a_n x + b_n)e^{-x}\).
- Expliciter \(a_n\)
- Vérifier que la suite \(c_n = (-1)^n b_n\) est arithmétique. En déduire \(b_n\).