3 février 2020
Introduction
Avant propos
L’objectif de ce cours est de comprendre l’intégrale. On présente souvent l’intégrale sous forme d’aire ou d’une primitive. Ces deux interprétations ne sont pas fausses mais masquent la nature fondamentale des intégrales
Plus précisément une somme de très nombreux éléménts (une infinité d’éléments) qui sont tous très petits (infinitésimaux). Il est souvent
Intuition géométrique
Soit \(f\) une fonction continue sur un segment \([a,b]\) (avec \(a \leq b\)). On appelle intégrale de \(a\) à \(b\) de \(f\) l’aire située entre
- la courbe de \(f\)
- l’axe des abscisses
- les droites d’équation \(x=a\) et \(x=b\).
en attribuant un signe négatif aux parties situées sous l’axe des abscisses. L’intégrale sur \([a,b]\) de \(f\) est notée \(\int_a^b f(x)dx\)
On pose par convention (pour généraliser la notion) \[ \int_b^a f(x)dx = - \int_a^b f(x)dx \]
Remarque La variable \(x\) est muette mais on intègre
Intuition géométrique (II)
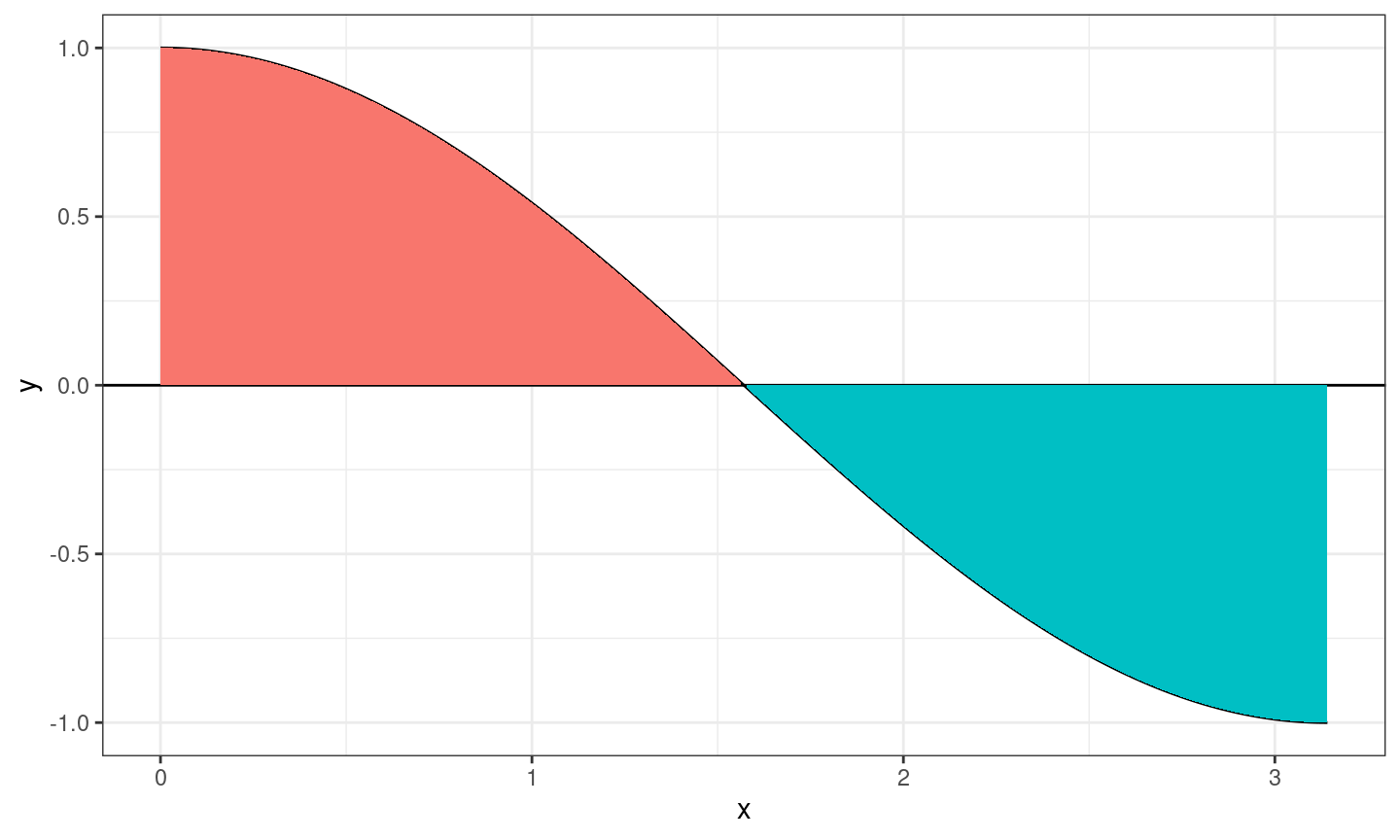
Théorème fondamental du calcul intégral
L’aire rouge compte positivement, l’aire bleue négativement.
Soit \(f\) une fonction continue sur un segment \([a,b]\) et \(F\) une primitive de \(f\) sur \([a,b]\). On a alors \[ \int_a^b f(x)dx = F(b) - F(a) = [F(x)]_a^b \]
Remarques sur le théorème
Le Théorème fondamental du calcul intégral est indispensable, en pratique, pour calculer des intégrales mais ne renseigne pas
- sur le lien entre intégrale et somme,
- sur la façon dont on utilise les intégrales dans de nombreuses situations.
Primitives usuelles
On rappelle quelques primtives usuelles (qui se déduisent des dérivées usuelles)
\[ \begin{array}{|c||c|} \hline \text{Fonction } f & \text{Primitive } F \\ \hline x^\alpha \quad (\alpha \neq -1) & x^{\alpha+1} / {(\alpha + 1}) \\ \hline 1 / x & \ln(x) \\ \hline e^x & e^x \\ \hline \cos(x) & \sin(x) \\ \hline \sin(x) & -\cos(x) \\ \hline \frac{1}{\sqrt{1 - x^2}} & \arcsin(x) \\ \hline \frac{-1}{\sqrt{1 - x^2}} & \arccos(x) \\ \hline \frac{1}{1+x^2} & \arctan(x) \\ \hline \end{array} \]
Recherche de Primitives (I)
Contrairement à la dérivation, il y a peu de régles automatiques pour trouver des primitives, la seule qui fonctionne est la régle d’addition
Soit \(f\) et \(g\) deux fonctions continues sur un segment \([a,b]\) dont \(F\) et \(G\) sont deux primitives. \(F+G\) est alors une primitive de \(f+g\) sur le segment \([a, b]\).
Mais on ne sait pas faire mieux, en particulier multiplier, quotienter, composer, etc…
Si on n’a pas affaire à une fonction de primitive astucieuse, il faut être astucieux et reconnaître une forme détournée, souvent cachée par un changement de variable.
Recherche de Primitives (II)
Les changements de variables classiques sont les suivants:
\[
\begin{array}{|c||c|}
\hline
\text{Fonction } f & \text{Primitive } F \\
\hline
u'(x) u(x)^\alpha \quad (\alpha \neq -1) & \frac{u(x)^{\alpha+1}}{(\alpha + 1)} \\
\hline
\frac{u'(x)}{u(x)} & \ln|u(x)| \\
\hline
u'(x) e^{u(x)} & e^{u(x)} \\
\hline
u'(x) \cos(u(x)) & \sin(u(x)) \\
\hline
u'(x) \sin(u(x)) & -\cos(u(x)) \\
\hline
\end{array}
\] Le but du jeu est bien sûr d’identifier la bonne fonction \(u(x)\) qui permet de se ramener au tableau précédent et attention à la
Exercice (I)
Trouver une primitive des fonctions (de \(x\)) suivantes (avec \(a \neq 0\)): \[ \begin{align*} f(x) = 1 - \frac{x^2}{2} & & f(x) = x^2 / (1+x^3) \\ f(x) = \frac{x^3}{2} + \frac{3x^5}{4} & & f(x) = x^2 / \sqrt{1 + x^3} \\ f(x) = 1 / (ax + b) & & f(x) = x^2 \sqrt{1 + x^3} \\ f(x) = \cos(ax + b) & & f(x) = 1 / \sqrt{1 - x^2} \\ f(x) = e^{ax + b} & & f(x) = 1 / (1 + x^2) \end{align*} \]
Solutions (I)
Les primitives sont \[ \begin{align*} F(x) = x - \frac{x^3}{6} & & F(x) = \frac{1}{3} \ln|1+x^3| \\ F(x) = \frac{1}{8}(x^4 + x^6) & & F(x) = \frac{2}{3} (1+x^3)^{1/2} \\ F(x) = \frac{1}{a}\ln|ax+b| & & F(x) = \frac{2}{9} (1+x^3)^{3/2} \\ F(x) = \frac{1}{a}\sin(ax + b) & & F(x) = \arcsin(x) \\ F(x) = \frac{1}{a}e^{ax + b} & & F(x) = \arctan(x) \end{align*} \]
Exercice (II)
Calculer ces intégrales (en reconnaissant parfois des formes décrites dans Recherche de Primitives (II)) : \[ \begin{align*} \int_{1}^2 (1 - x + x^2 - x^3)dx & & \int_0^{\pi} \sin(x)dx \\ \int_{1}^4 \frac{dx}{\sqrt{x}} & & \int_{-\pi/2}^{\pi/2} \cos(x)dx \\ \int_0^1 \frac{dx}{1+x} & & \int_{0}^1 \frac{2xdx}{1+x^2} \\ \int_{1}^2 (1+x)^{\alpha}dx \quad (\alpha \neq -1) & & \int_{0}^1 x^2 e^{-x^3}dx \\ \int_0^2 e^x dx & & \int_1^e \frac{\ln(x)}{x}dx \end{align*} \]
L’intégrale comme une somme
Intégrale et Somme
Une intégrale est une
- le terme \(dx\) sous-entend une
variable \(x\) qui varie très lentement par petits pas de longueur \(dx\) entre \(a\) et \(b\). - le terme \(f(x)dx\) siginifie que les petits pas \(dx\) sont multipliés par un coefficient multiplicatif, \(f(x)\), qui varie lorsque \(x\) varie. Au début, le coefficient multiplicatif vaut \(f(a)\), à la fin \(f(b)\) et entre les deux, il varie comme \(f\).
- Le signe \(\int\) correspond au \(S\) allongé de Somme.
Il faut donc comprendre \(\int_{a}^b f(x)dx\) comme la somme de petites quantités \(f(x)dx\) obtenues en faisant varier \(x\) par petits pas \(dx\) entre \(a\) et \(b\).
Interprétation graphique
- Si \(f(x) > 0\), \(f(x)dx\) est l’aire du rectangle foncé
- Si \(f(x) < 0\), \(f(x)dx\) est l’opposé de la même aire.
Calcul d’une intégrale simple
On va calculer l’intégrale simple \(\int_{z_1}^{z_2} dz\). C’est la somme de toutes les petites variations \(dz\) lorsque \(z\) passe de la valeur initiale \(z_1\) à la valeur finale \(z_2\).
Quel que soit le chemin pris entre \(z_1\) et \(z_2\), en faisant la somme des petites variations successives, on obtient la variation totale, c’est à dire \(\Delta z = z_2 - z_1\).
Mais que faire quand on doit calculer une intégrale plus complexe du type \(\int_{z_1}^{z_2} f(z)dz\) avec \(f\) qui dépend de \(z\)?
Calcul d’une intégrale complexe
\(f(z)\) est un coefficient de proportionalité. La quantité \(f(z)dz\) est proportionnelle à \(dz\), on peut la comprendre comme la
En particulier, si on trouve une fonction \(F(z)\) telle que \(\frac{dF(z)}{dz} = f(z)\), c’est à dire une primitive de \(f\), on a alors la relation
\[ dF = f(z) dz \]
Calcul d’une intégrale complexe (II)
Ainsi, lorsque \(z\) varie entre \(z_1\) et \(z_2\) par petits pas \(dz\), la quantité \(F(z)\) varie par petits pas \(dF = f(z)dz\) entre une valeur initiale notée \(F_1 = F(z 1 )\) et une valeur finale \(F_2 = F(z_2)\).
La somme des petits éléments \(f(z)dz\) entre \(z_1\) et \(z_2\) est donc la même que celle des petits incréments \(dF\) entre \(F_1\) et \(F_2\).
\[ \int_{z_1}^{z_2} f(z)dz = \int_{F_1}^{F_2} dF = \Delta F = F_2 - F_1 \]
Primitive et forme différentielle
Les quantités infinitésimales ci-dessous sont de la forme \(f(x) dx\). Les exprimer sous la forme \(f (x)dx = dF\) , où \(F\) est par définition une primitive de \(f\). Par exemple, \(\cos(\theta) d\theta = d(\sin(\theta))\) car \(\frac{d\sin(\theta)}{d\theta} = \cos(\theta)\).
\[ \begin{align} -u e^{u^2} \text{d}u & & 3 \cos(\theta) \sin^2(\theta) \text{d} \theta \\ \left( v / \sqrt{1 - v^2} \right) \text{d} v & & x^{\alpha} dx \\ \sin(\alpha \varepsilon) \text{d} \varepsilon & & (y^3 \text{d}y) / (\alpha^4 + y^4)^2 \\ (1 + \tan^2(\alpha)) \text{d} \alpha & & \text{d} z / ( 1 + a z) \quad (a \neq 0) \end{align} \]
Primitive et forme différentielle (II)
\[ \begin{align} -u e^{u^2} \text{d}u = d(-e^{u^2}/2)& & 3 \cos(\theta) \sin^2(\theta) \text{d} \theta = d(\sin^3(\theta)) \\ \left( \frac{v}{\sqrt{1 - v^2}} \right) \text{d} v =d(-\sqrt{1-v^2}) & & x^{\alpha} dx = d\left(\frac{x^{\alpha+1}}{\alpha+1} \right)\\ \sin(\alpha \varepsilon) \text{d} \varepsilon = d\left(\frac{-\cos(\alpha \varepsilon)}{\alpha} \right)& & \frac{y^3 \text{d}y}{(\alpha^4 + y^4)^2} = d\left( \frac{-1}{4(\alpha^4 + y^4)}\right)\\ (1 + \tan^2(\alpha)) \text{d} \alpha = d(\tan(\alpha)) & & \text{d} z / ( 1 + a z) = d\left( \frac{\ln|1+az|}{a} \right) \end{align} \]
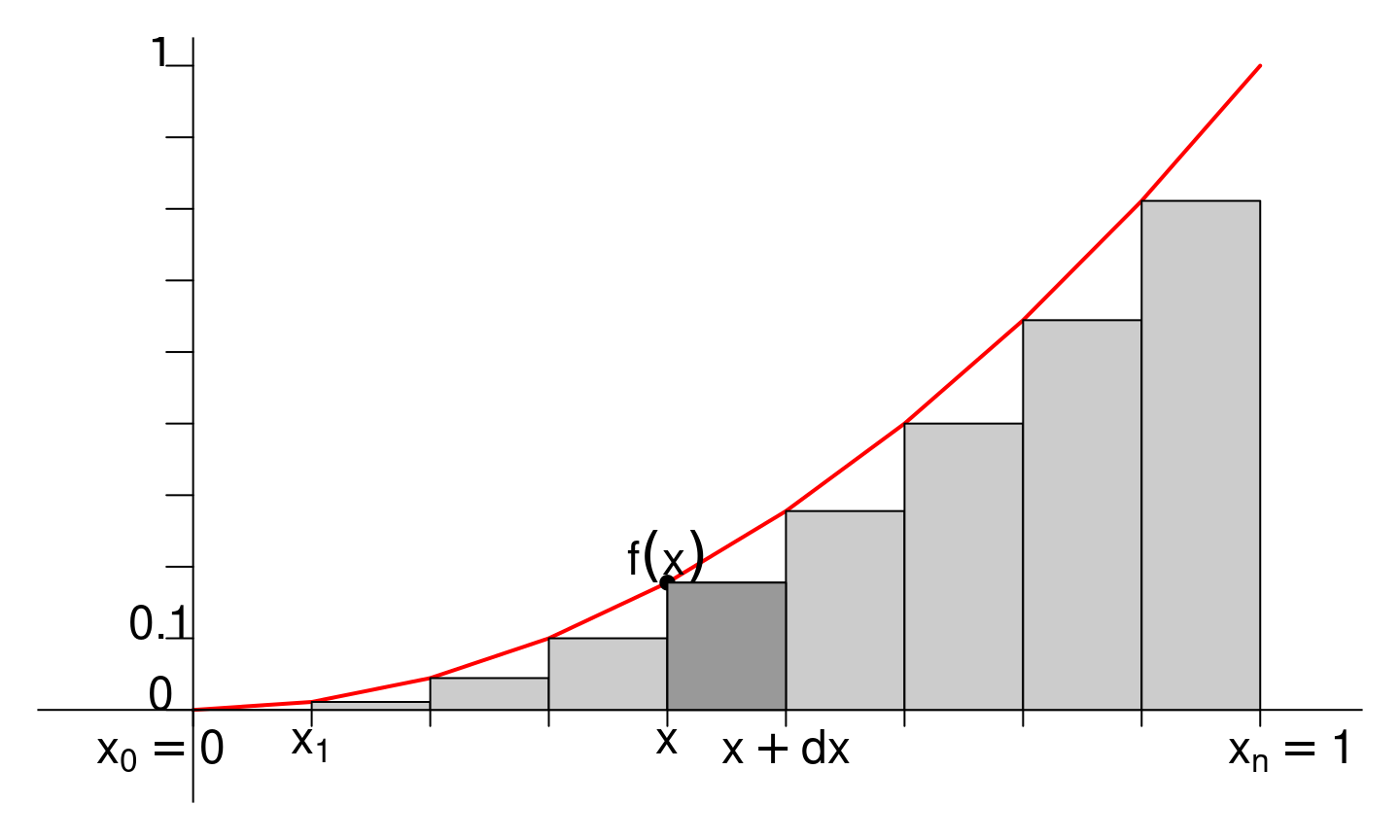
Sommes de Riemann
Soit \(f\) une fonction continue sur un segment \([a, b]\). On va considérer des pas \(dx\) bien choisis, de la forme \(\frac{b - a}{n}\). Posons
\[ x_0 = 1, x_1 = a + \frac{b-a}{n}, ..., x_n = a + n\frac{b-a}{n} = b \] L’aire de chaque rectangle \(f(x)dx\) est donc \(f(x_k) \frac{b-a}{n}\) (en fonction du point \(x_k\) où on l’évalue) et leur somme vaut \[ S_n = \sum_{k = 0}^{n-1} f(x_k) dx = \sum_{k = 0}^{n-1} f(x_k) (x_{k+1} - x_k) = \sum_{k = 0}^{n-1} f(x_k) \frac{b-a}{n} \]
Sommes de Riemann (II)
D’après la définition de l’intégrale, on devrait avoir \(S_n \simeq \int_{a}^b f(x)dx\) et on a effectivement le théorème suivant:
Soit \(f\) une fonction continue sur un segment \([a,b]\). Pour tout \(n \geq 1\), on pose \[ S_n = \frac{b-a}{n} \sum_{k = 0}^{n-1} f \left( a + k \frac{b-a}{n} \right) \] Alors \[ S_n \xrightarrow[n \to \infty]{} \int_{a}^b f(x)dx \]
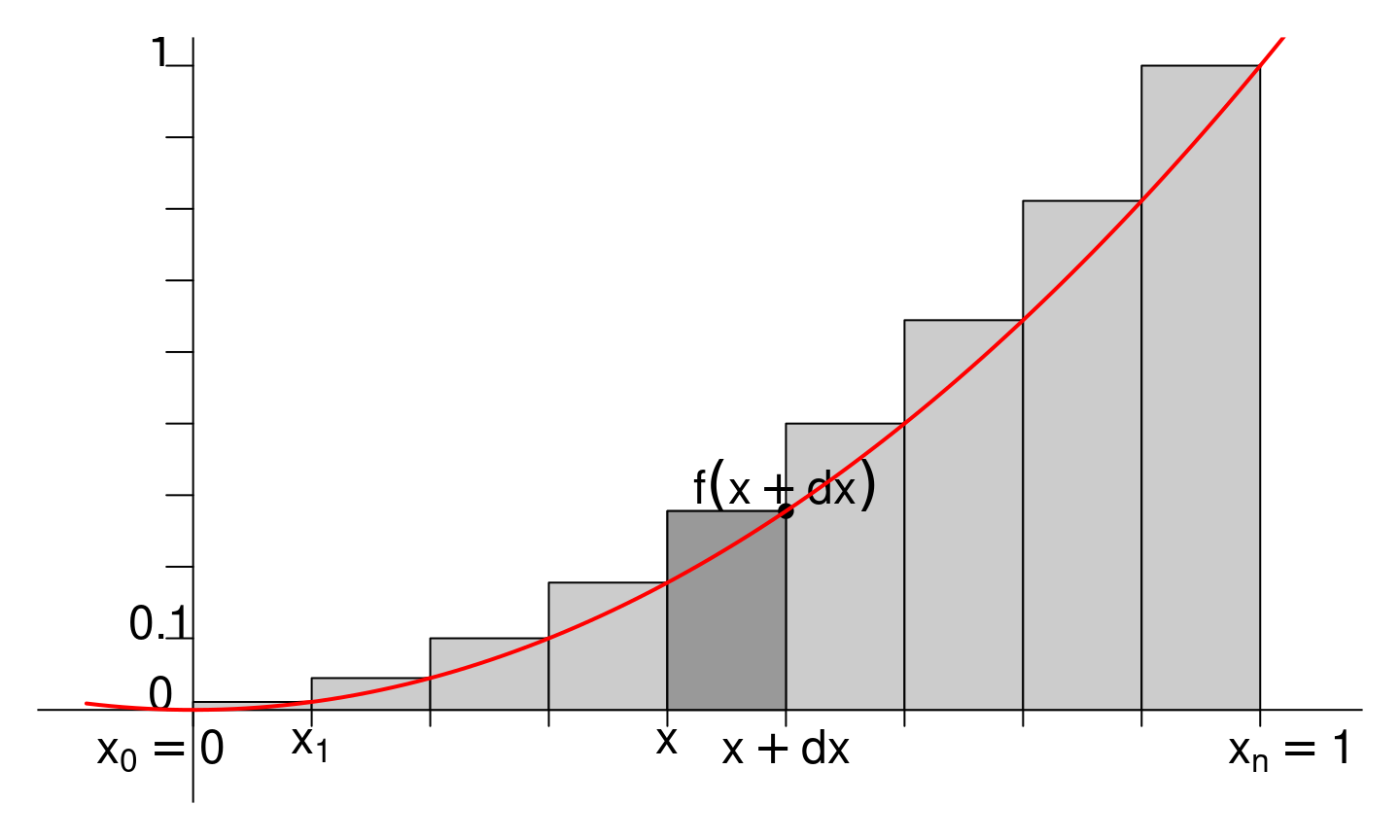
Sommes de Riemann (IV)
On peut également construire d’autres suites de rectangles qui donnent une somme de Riemann qui convergent vers la même quantité:
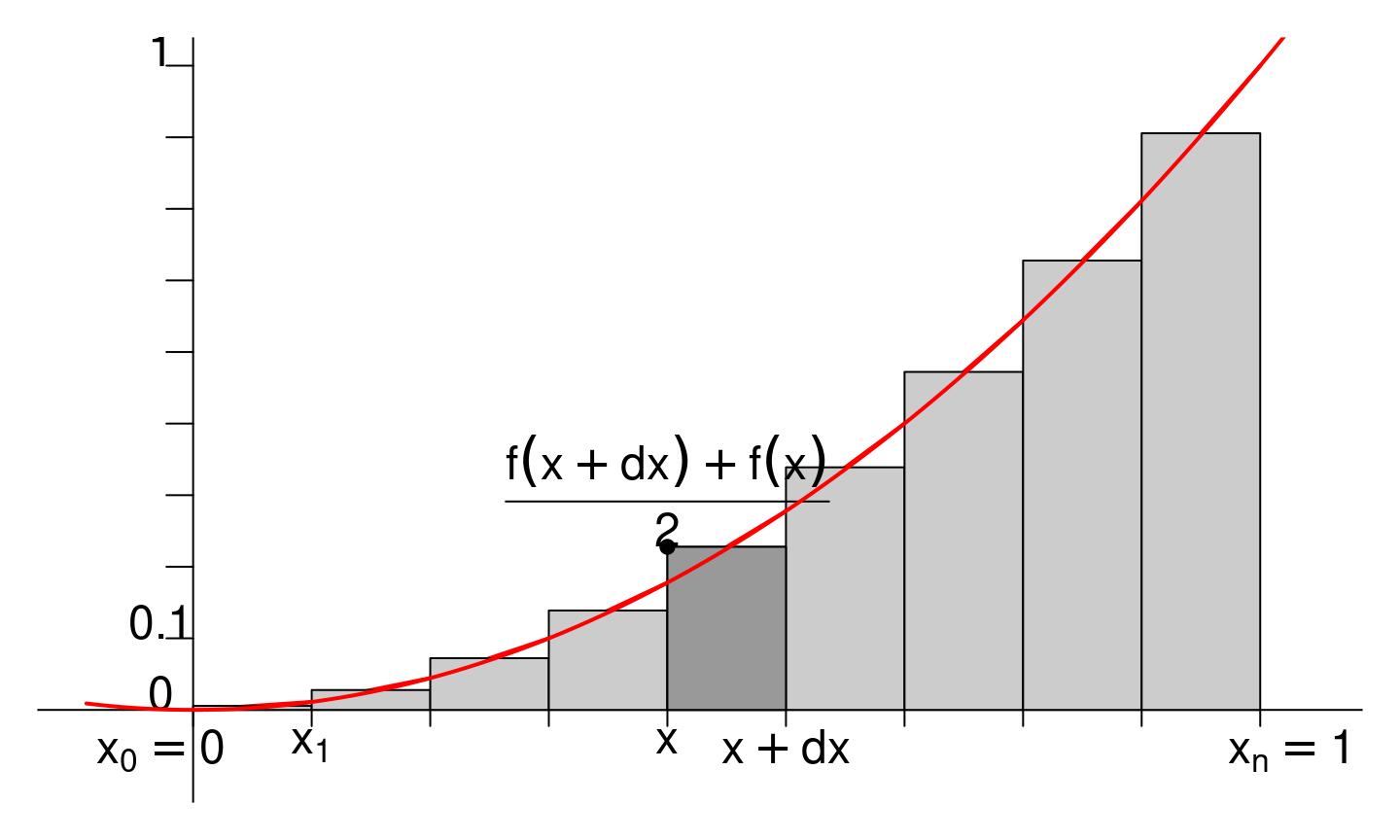
Sommes de Riemann (V)
On peut également construire d’autres suites de rectangles qui donnent une somme de Riemann qui convergent vers la même quantité:
Sommes de Riemann (VI)
En particulier, on peut considérer les rectangles d’aires \[
\begin{align}
\mathcal{A}_k & = (x_{k+1} - x_{k}) f(x_k) = \frac{b-a}{n} f\left( a + k \frac{b-a}{n} \right) \\
\mathcal{B}_k & = (x_{k+1} - x_{k}) f(x_{k+1}) = \frac{b-a}{n} f\left( a + (k+1) \frac{b-a}{n} \right) \\
\mathcal{C}_k & = (x_{k+1} - x_{k}) \frac{f(x_{k}) + f(x_{k+1})}{2} \\
& = \frac{b-a}{n} \frac{f\left( a + k \frac{b-a}{n} \right) + f\left( a + (k+1) \frac{b-a}{n} \right)}{2}
\end{align}
\] Et obtenir 3 sommes de Riemann différentes qui convergent toutes vers la
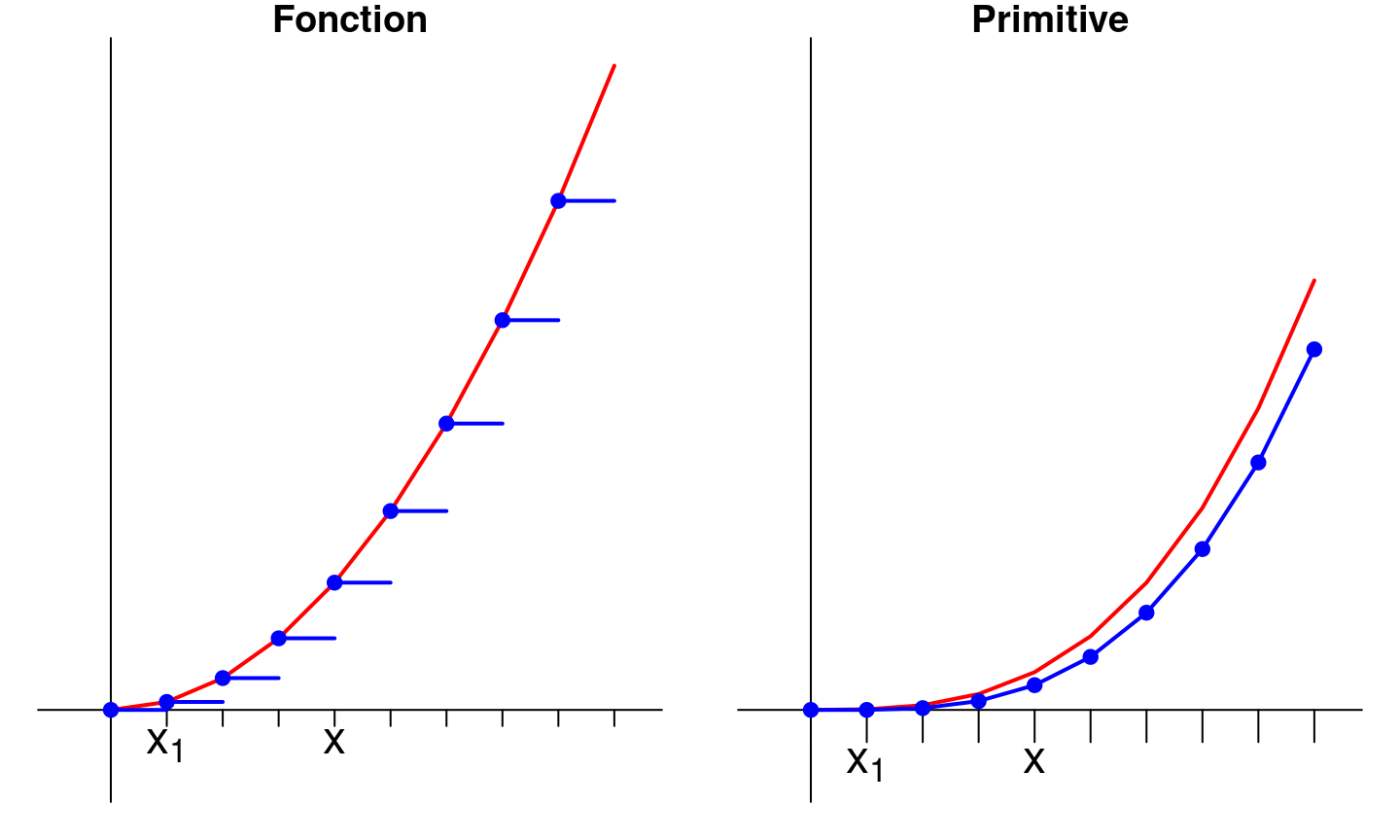
Interprétation graphique (I)
L’approximation \(f(x)dx \simeq f(x_k) (x_{k+1} - x_{k})\) revient à:
- considérer que \(f\) est constante sur \([x_k, x_{k+1}]\)
- que la primitive \(F\) de \(f\) est affine, de pente \(f(x_k)\) sur \([x_k, x_{k+1}]\)
Interprétation graphique (II)
Approximation pour \(n = 10\)
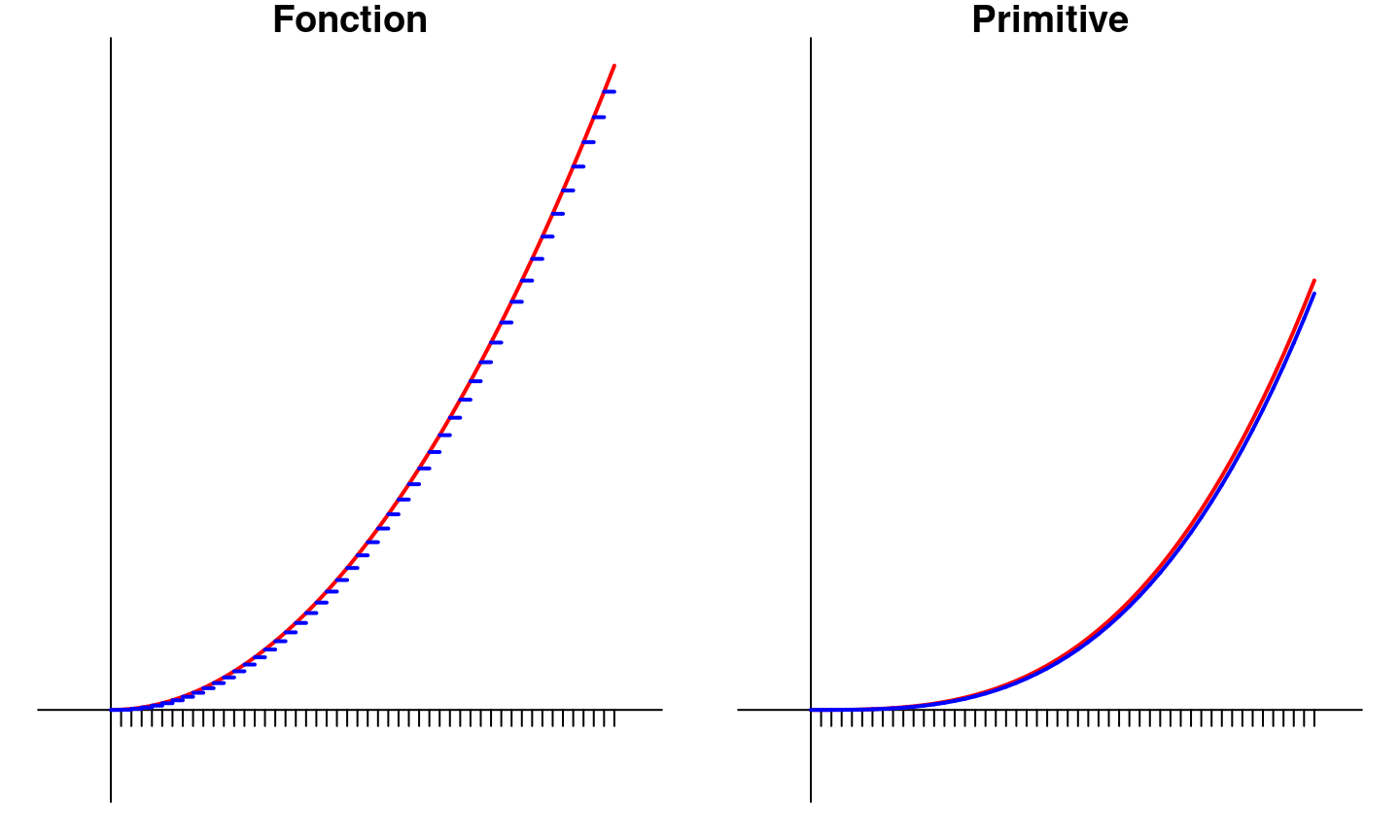
Interprétation graphique (III)
Approximation pour \(n = 50\) (Meilleure)
Exercices (I)
Vérifier que les sommes suivantes sont bien des sommes de Riemann (c’est à dire peuvent s’écrire sous la forme \(\frac{b-a}{n} \sum f(x_k)\) avec \(f, a, b\) à déterminer) et calculer leurs limites \[ \begin{align} A_n = \sum_{k = 0}^{n-1} \frac{k}{n^2} & & B_n = \sum_{k = 1}^n \frac{k}{n^2} \\ C_n = \sum_{k = 0}^{n-1} \frac{k}{k^2 + n^2} & & D_n = \sum_{k = 1}^n \frac{1}{n+k} \end{align} \]
Exercices (I) : Réponses
Pour toutes les sommes de Riemann, on a \(a = 0\) et \(b = 1\). \[ \begin{align} A_n = \sum_{k = 0}^{n-1} \frac{k}{n^2} \rightarrow \int_0^1 xdx & & B_n = \sum_{k = 1}^n \frac{k}{n^2} \rightarrow \int_0^1 xdx \\ C_n = \sum_{k = 0}^{n-1} \frac{k}{k^2 + n^2} \rightarrow \int_0^1 \frac{xdx}{1+x^2} & & D_n = \sum_{k = 1}^n \frac{1}{n+k} \rightarrow \int_0^1 \frac{dx}{1+x} \end{align} \]
Exercices (II)
Même consigne (mais attention, ici on n’a pas forcément \(a = 0\) et \(b = 1\))
\[ \begin{align} E_n = \sum_{k = 0}^{n-1} \frac{1}{\sqrt{n^2 - k^2}} & & F_n = \sum_{k = 1}^n \frac{n}{{n^2 + k^2}} \\ G_n = \sum_{k = 0}^{n-1} \frac{k}{n\sqrt{n^2 - k^2}} & & H_n = \sum_{k = 1}^n \frac{k^2}{n^3} \end{align} \]
Exercices (II) : Réponses
\[ \begin{align} E_n & = \sum_{k = 0}^{n-1} \frac{1}{\sqrt{n^2 - k^2}} = \frac{1}{n} \sum_{k=0}^{n-1} \frac{1}{\sqrt{1 - (k/n)^2}} \to \int_0^1 \frac{dx}{\sqrt{1 - x^2}} = [\arcsin(x)]_0^1 = \frac{\pi}{2}\\ F_n & = \sum_{k = 1}^n \frac{n}{{n^2 + k^2}} = \frac{1}{n} \sum_{k=1}^{n} \frac{1}{1 + (k/n)^2} \to \int_0^1 \frac{dx}{1 + x^2} = [\arctan(x)]_0^1 = \frac{\pi}{4} \\ G_n & = \sum_{k = 0}^{n-1} \frac{k}{n\sqrt{n^2 - k^2}} = \frac{1}{n} \sum_{k=0}^{n-1} \frac{k/n}{\sqrt{1 - (k/n)^2}} \to \int_0^1 \frac{xdx}{\sqrt{1 - x^2}} =\left[-\sqrt{1-x^2}\right]_0^1 = 1 \\ H_n & = \sum_{k = 1}^n \frac{k^2}{n^3} = \frac{1}{n} \sum_{k=1}^{n} (k/n)^2 \to \int_0^1 x^2dx = \left[ \frac{x^3}{3}\right]_0^1 = \frac{1}{3} \end{align} \]
Propriétés de l’intégrale
Linéarité
Soit \(f, g\) deux fonctions continues sur un segment \([a,b]\) et \(\lambda \in \mathbb{R}\). \[ \begin{align} \int_{a}^b f(t) + g(t)dt & = \int_a^b f(t)dt + \int_a^b g(t)dt \\ \int_a^b \lambda f(t)dt& = \lambda \int_a^b f(t)dt \end{align} \]
Relation de Chasles
Soit \(f\) continue sur un segment \([a,b]\) et \((x, y, z) \in [a, b]\) (quel que soit leur ordre) \[ \int_x^z f(t)dt = \int_x^y f(t)dt + \int_y^z f(t)dt \]
On n’a pas besoin d’avoir \(x \leq y \leq z\) mais il faut que \(f\) soit bien continue sur les intervalles \([x, y]\), \([y, z]\), \([x, z]\) (avec les bornes éventuellement réordonnées).
Positivité et croissance
Soit \(f\) et \(g\) continues sur \([a,b]\) et
- \(f\) est
positive , alors \[ \int_a^b f(t)dt \geq 0 \] - Si \(f(x) \leq g(x)\) pour tout \(x \in [a, b]\) alors \[ \int_a^b f(t)dt \leq \int_a^b g(t)dt \]
Passage à la valeur absolue
Soit \(f\) continue sur \([a,b]\) et
Encadrement
Soit \(f\) continue sur \([a,b]\) et
Valeur moyenne d’une fonction
Soit \(f\) continue sur \([a,b]\) et
C’est l’équivalent du théorème des acroissements finis, reformulé avec des intégrales plutôt qu’avec des dérivées.
Techniques de calcul
Intégration par parties (IPP)
L’idée d’une IPP est de profiter de la formule de dérivation d’un produit: \((fg)' = f'g + fg'\). Si on a deux fonctions de classe \(\mathcal{C}^1\) sur \([a, b]\), on sait que: \[ \int_a^b (fg)'(t) dt = [f(t)g(t)]_a^b \] Mais on sait aussi que \[ \int_a^b (fg)'(t) dt = \int_a^b f'(t)g(t) dt + \int_a^b f(t)g'(t) dt \]
Intégration par parties (IPP) (II)
Soit \(f\), \(g\) de classe \(\mathcal{C}^1\) sur \([a,b]\). On a alors \[ \int_a^b f'(t)g(t) dt = [f(t)g(t)]_a^b - \int_a^b f(t)g'(t) dt \]
Lorsqu’on fait une IPP, il est recommandé de bien préciser \(f, g, f', g'\).
IPP: Exemple
On cherche à calculer \(A = \int_0^1 xe^{x}dx\). On sait facilement intégrer et dériver \(e^x\) et \(x\) donc deux choix s’offrent à nous:
- Poser \(f'(x) = x\) et \(g(x) = e^x\). Mais on devra calculer \(\int_0^1 f(x)g'(x)dx = \int_0^1 \frac{x^2}{2} e^x dx\)…
- Poser \(f'(x) = e^{x}\) et \(g(x) = x\). On devra calculer \(\int_0^1 f(x)g'(x)dx = \int_0^1 e^x dx\). C’est mieux.
IPP: Exemple (II)
On pose donc \(f'(x) = e^{x}\) et \(g(x) = x\) d’où on tire \(f(x) = e^x\) et \(g'(x) = 1\) et on injecte dans la formule: \[ \begin{align} \int_0^1 xe^{x} dx & = \int_0^1 g(x)f'(x) dx \\ & = [g(x)f(x)]_0^1 - \int_0^1 g'(x)f(x) dx \\ & = [xe^x]_0^1 - \int_0^1 e^xdx = [xe^x]_0^1 - [e^x]_0^1 \\ & = e - (e - 1) = 1 \end{align} \]
Les IPP sont surtout utiles pour les intégrales de fonction du type \(x^k e^x\), \(x^k \cos(x)\) et \(\cos(x)e^x\).
IPP: Exercices
Calculer les intégrales suivantes à l’aide d’une ou plusieures IPP
\[ \begin{align} A = \int_{-1}^1 xe^{3x}dx & & B = \int_0^1 y^4 e^y dy \\ C = \int_{0}^1 (t^2 + t)e^{2t} dt & & D = \int_{1}^e 1.\ln(x) dx \\ E_n = \int_{1}^e u^n \ln(u) du \quad (n \in \mathbb{N}) & & F = \int_{\sqrt{e}}^e \frac{\ln(v)}{v}dv \\ G = \int_{1}^{e^2} (2x^3 + 1) \ln(x)dx & & H = \int_1^4 \sqrt{3s} \ln(s) ds \end{align} \]
IPP: Solutions
Calculer les intégrales suivantes à l’aide d’une ou plusieures IPP
\[ \begin{align} A = \frac{2}{9}(e^3 + 2e^{-3}) & & B = 9e - 24 \\ C = (e^2-1)/2 & & D = 1 \\ E_n = \frac{1}{(n+1)^2}\left[ ne^{n+1} + 1 \right] & & F = 3/8 \\ G = \frac{1}{8}(7e^8 + 1) + (e^2 + 1) & & H = \frac{4}{\sqrt{3}} \left[ 8\ln(2) - \frac{7}{3}\right] \end{align} \]
Corrections détaillées disponibles ici
IPP: Exercices (II)
Calculer les intégrales suivantes à l’aide d’une ou plusieures IPP (et éventuellement d’un peu de linéarisation…)
\[ \begin{align} A = \int_{0}^{\pi/2} \cos(x)e^x dx & & B = \int_0^{\pi/2} \sin(x)e^x dx \\ C = \int_{0}^1 x^2\cos(x) dx & & D = \int_{0}^1 x^2 \cos^2(x)dx\\ \end{align} \]
Corrections détaillées disponibles ici
Changement de variables
Soit \(f\) continue sur \([a,b]\) et \(\phi\) une fonction \(\mathcal{C}^1\) d’un intervalle \([\alpha, \beta]\) dans \([a, b]\) telle que \(\phi(\alpha) = a\) et \(\phi(\beta) = b\). Alors on peut effectuer le changement de variables \(x = \phi(t)\) de la façon suivante \[ \int_a^b f(x) dx = \int_{\alpha}^{\beta} f(\phi(t)) \phi'(t) dt \]
En pratique
Quand on change de variable, on a trois éléments à changer:
la variable: (ça va sans dire…) Il faut remplacer toutes les occurences de \(x\) par leur expression \(\phi(t)\)les bornes quand \(x\) varie entre \(a\) et \(b\), \(t\) varie entre \(\alpha\) et \(\beta\). Comme \(x = \phi(t)\), on doit avoir \(a=\phi(\alpha)\) et \(b = \phi(\beta)\) et il faut donc trouver un \(\alpha\) et un \(\beta\) convenable.l’élement différentiel \(dx\) Comme on intègre par rapport à \(t\), il faut remplacer \(dx\) par une expression qui fait intervenir \(dt\). Comme \(x = \phi(t)\), on sait que \(\frac{dx}{dt} = \phi'(t)\), c’est à dire \(dx = \phi'(t) dt\).
En pratique, on utilise souvent la formule “de la droite vers la gauche”. Intuitivement, les deux intégrales sont égales parce qu’on somme des petits éléments égaux: \[ f(x)dx = g(t)dt \; [ = f(\phi(t)) \phi'(t) ] \]
Changement de variable: exemple
On cherche à calculer \(I = \int_1^e \frac{\ln(t)}{t}dt\) à l’aide du changement de variable \(x = \ln(t)\). On effectue les trois changements.
- On change la variable: \(\frac{\ln(t)}{t} = x/e^x\)
- On change les bornes: quand \(t\) varie entre \(1\) et \(e\), \(x = \ln(t)\) varie entre \(0\) et \(1\).
- On change l’élément différentiel: \(t = e^x\) donc \(dt = e^x dx\)
\[ \begin{align} I & = \int_{t = 1}^{t = e} \frac{\ln(t)}{t}dt = \int_{x = 0}^{x = 1} \frac{x}{e^x} e^x dx = \int_0^1 xdx = 1/2 \end{align} \]
Deuxième exemple (I)
On veut calculer l’intégrale \(I = \int_{\pi/6}^{\pi/3} \frac{\cos(\theta)}{\sin(\theta)} d\theta\). On remarque au numérateur une différentielle connue puisque \(\cos(\theta) d\theta = d(\sin(\theta))\). Il est donc tentant d’essayer de tout écrire en fonction de \(y = \sin(\theta)\).
- Concernant l’élément différentiel, on sait que \(dy = \cos(\theta) d\theta\)
- On veut réécrire l’expression dans l’intégrale en fonction de \(y\) seulement: \(\frac{\cos(\theta)}{\sin(\theta)} d\theta = \frac{dy}{\sin(\theta)} = \frac{dy}{y}\)
- On veut changer les bornes, quand \(\theta = \pi/6\), \(y = \sin(\pi/6) = 1/2\) et quand \(\theta = \pi/3\), \(y = \sin(\pi/6) = \sqrt{3}/2\)
Deuxième exemple (II)
On a donc
\[ \begin{align} I & = \int_{\theta = \pi/6}^{\theta = \pi/3} \frac{\cos(\theta)}{\sin(\theta)}d\theta \\ & = \int_{y = 1/2}^{y = \sqrt{3}/2} \frac{dy}{y} \\ & = [\ln(y)]_{1/2}^{\sqrt{3}/2} = \ln(\sqrt{3}) \end{align} \]
Troisième exemple (I)
On cherche à calculer l’intégrale \(\int_{0}^{\pi/2} \sin^{3}(\alpha) d\alpha\) avec le changement de variable \(u = \cos(\alpha)\)
- Concernant l’élément différentiel, on sait que \(du = -\sin(\alpha) d\alpha\)
- On veut réécrire l’expression dans l’intégrale en fonction de \(u\) uniquement: \[ \begin{align} \sin^{3}(\alpha)d\alpha & = \sin^2(\alpha) \sin(\alpha) d\alpha = - \sin^2(\alpha) du \\ & = -(1 - \cos^2(\alpha)) du = - (1 - u^2)du \end{align} \]
- On veut changer les bornes,
- quand \(\alpha = 0\), \(u = \cos(\alpha) = \cos(0) = 1\)
- quand \(\alpha = \pi/\), \(u = \cos(\alpha) = \cos(\pi/2) = 0\)
Troisième exemple (II)
On a donc
\[ \begin{align} I & = \int_{\alpha = 0}^{\alpha = \pi/2} \sin^3(\alpha) d\alpha \\ & = \int_{u = 1}^{u = 0} -(1 - u^2)du \\ & = \int_{u = 0}^{u = 1} (1 - u^2)du \\ & = \left[u - \frac{u^3}{3}\right]_{0}^1 = \frac{2}{3} \end{align} \]
Changement de variable: exercices
Calculer les intégrales suivantes à l’aide du changement de variable proposé: \[ \small \begin{align} \int_{\pi/4}^{\pi/3} \tan(\theta) d\theta & & \text{en posant } v = \cos(\theta) \\ \int_{0}^{\pi/2} \cos^3(\theta) d\theta & & \text{en posant } v = \sin(\theta) \\ \int_0^{\pi / \omega} \cos\left( \frac{\pi}{3} - \frac{\omega t }{2}\right)dt & & \text{en posant } y = \frac{\pi}{3} - \frac{\omega t}{2} \\ \int_{x_0}^{x_0 + H} (x - x_0) e^{- \left( \frac{x - x_0}{h} \right)^2} dx& & \text{en posant } z = \left(\frac{x - x_0}{h}\right)^2 \\ \int_0^R \frac{dr}{(R^2 + r^2)^{3/2}} & & \text{en posant } r = R\tan(\alpha) \end{align} \]
Corrections détaillées disponibles ici
Changement de variable: exercices (II)
Calculer les intégrales suivantes:
\[ \small \begin{align} \int_{0}^{1} w \sqrt{3w+1} dw & & \text{en posant } z = 3w+1 \\ \int_{0}^{1} \frac{dx}{e^x + 1} & & \text{en posant } v= e^x [*] \\ \int_1^{2} \frac{ds}{s(s^3+1)} & & \text{en posant } y = s^3 + 1 [*]\\ \int_{-1}^{0} \frac{u^3 du}{(u^2 + 1)\sqrt{u^2 +1}} & & \text{en posant } v = u^2 + 1 \\ \int_0^3 \frac{t \ln(t^2 + 1)}{t^2 + 1}dt & & \text{en posant } x = t^2 + 1 \end{align} \]
\([*]\) On peut utiliser le fait que \(1/(x(x-1)) = 1/(x-1) - 1/x\) et \(1/(x(x+1)) = 1/x - 1/(x+1)\).
Corrections détaillées disponibles ici
Intégrale à borne variable
Un problème de notation
Jusqu’à présent, on a uniquement des intégrales de la forme \(I = \int_{x_0}^{x_1} f(x)dx\) mais rien n’oblige les deux bornes à être des constantes. On pourrait avoir envie de faire varier la valeur finale (\(b\)) et de l’appeler \(x\).
Ici on a donné le même nom \(x\)à deux choses différentes:
- la quantité qui varie par petit pas et qu’on utilise pour faire une grande somme de petits éléments;
- la valeur finale pour laquelle on arrête de sommer.
Solution
Pour lever l’incertitude, on donne un nom différent à la
\[ I(x) = \int_{x_0}^x f(t)dt \]
Le résultat de l’intégration n’est plus un nombre bien défini mais une valeur qui dépend de \(x\), c’est une fonction, notée \(I(x)\). Si \(F\) est une primitive de \(f\), on peut en effet écrire \[ I(x) = \int_{x_0}^x f(t)dt = F(x) - F(x_0) \]
En particulier \(I(x)\) est
Exemple
Un mobile se déplace sur une droite en partant du point \(x = 0\). Sa vitesse au temps \(t\) est notée \(v(t)\). On sait alors que sa position au temps \(t\) est donnée par \[ x(t) = \int_0^t v(z)dz \]
Comparaison somme - intégrale
À savoir
Soit \(f\) positive, continue et
- elle diverge si \(\int_{1}^n f(x)dx\) diverge (car minorée par une suite divergente)
- elle converge si \(\int_{1}^\infty f(x)dx\) existe (car croissante et majorée).
En résumé \(S_n\) converge quand \(n \to +\infty\)
Note Si \(f\) n’est pas intégrale en \(0\), on peut remplacer le terme de droite par \(f(1) + \int_1^{n} f(x)dx\).
Démonstration
La preuve est basée sur l’idée suivante (à retenir car très puissante et facile à réutiliser): pour tout \(n \geq 1\) et \(x \in [n-1, n]\), on a
\[ f(n) \leq f(x) \leq f(n-1) \] par décroissance de \(f\). En intégrant par rapport à \(x\) sur \([n-1, n]\), on obtient donc \[ \int_{n-1}^n f(n)dx \leq \int_{n-1}^n f(x)dx \leq \int_{n-1}^n f(n-1)dx \Rightarrow f(n) \leq \int_{n-1}^n f(x)dx \leq f(n-1) \] qu’on peut réécrire \[ \int_{n}^{n+1} f(x)dx \leq f(n) \leq \int_{n-1}^n f(x)dx \] Il suffit ensuite de sommer et d’utilise la relation de Chasles pour conclure.
Exercices
- En utlisant une comparaison somme intégrale, montrer que la suite \(S_n(\alpha) = \sum_{i=1}^n \frac{1}{i^\alpha}\) converge
si et seulement si \(\alpha > 1\). - Trouver un équivalent de la suite \(H_n = S_n(1)\) (aussi appelée série harmonique), c’est à dire une fonction simple \(f(n)\) telle que \(H_n / f(n) \to 1\) quand \(n \to \infty\)
Solutions
En appliquant le résultat précédent à la fonction \(f: x \mapsto x^{-\alpha}\) on montre \[ \int_1^{n+1} x^{-\alpha} dx \leq S_n(\alpha) \leq 1 + \int_1^{n} x^{-\alpha} dx \] On cherche donc à savoir si \(I_n = \int_1^n x^{-\alpha}dx\) converge quand \(n \to \infty\) \[ I_n = \begin{cases} \ln(n) & \text{si } \alpha = 1 \\ \frac{n^{1 - \alpha} - 1}{1-\alpha} & \text{si } \alpha \neq 1\end{cases} \] En utilisant les limites classiques des fonctions puissances et logarithmes, on montre que \(I_n \to \infty\) si et seulement si \(\alpha \leq 1\). On en déduit que \(S_n(\alpha)\) converge si et seulement si \(\alpha > 1\).
Solutions II
En reprenant l’encadrement précédent pour \(\alpha = 1\), on montre que \(H_n = S_n(1)\) vérifie l’encadrement \[ \ln(n+1) \leq H_n \leq 1 + \ln(n) \] Par théorème d’encadrement, \(\frac{H_n}{\ln(n)} \to 1\), qu’on écrit de façon compacte \(H_n \sim \ln(n)\) (c’est ce qu’on appelle un développement asymptotique de \(H_n\))
Problème du chasse-neige
Énoncé
Il a commencé à neiger à un rythme soutenu ce matin. Un chasse neige a commencé à déneiger la route à 12h. Il a déneigé 2 km la première heure et 1 kilomètre la deuxième heure. À quelle heure a-t-il commencé à neiger?
Solution (I)
On va essayer de “formaliser” l’énoncé pour le traduire en langage mathématiques et trouver la solution. On va faire quelques hypothèses:
- la neige tombe à rythme constant \(\rho\)
- la quantité de neige accumulée \(n\) est proportionnelle au temps écoulé depuis qu’il a commencé à neiger
- la vitesse \(v\) du chasse-neige est inversement propotionnelle à la quantité de neige accumulée
- on mesure le temps \(t\) (en heure) à partir de midi et on note \(T\) le temps écoulé (à midi depuis le début des chutes)
Avec tous ces élements en main, on va écrire des relations entre les différentes quantités du problème.
Solution (II)
- Au temps \(t\), il neige depuis \(T+t\) heures et la neige accumulée en une portion de route non déblayée est donc \(n(t) = \rho(T+t)\)
- Lorsque le chasse neige déblaie cette portion, il le fait à vitesse \(v(t) = v_0 / \rho(T+t)\) (\(v_0\) correspond en un sens à l’efficacité du chasse-neige).
- La distance \(dx\) parcourue par le chasse-neige entre les temps \(t\) et \(t + dt\) est donc \(dx = v(t)dt\).
En intégrant, on trouve que la position \(x(u)\) du chasse neige au temps \(u\) est \[ x(u) = \int_0^u dx = \int_0^u v(t)dt = \int_0^u \frac{v_0dt}{\rho(t+T)} = \frac{v_0}{\rho}[\ln|t+T|]_0^u = \frac{v_0}{\rho}\ln\frac{u+T}{T} \] D’après l’énoncé \(x(1) = 2\) et \(x(2) = 3\). On a donc \[ 2x(2) = 3x(1) \Leftrightarrow 2\ln\frac{2+T}{T} = 3\ln\frac{1+T}{T} \Leftrightarrow \left(\frac{2+T}{T} \right)^2 = \left( \frac{1+T}{T} \right)^3 \]
Solution III
En continuant les calculs, on obtient
\[ \begin{align} T(2+T)^2 = (1+T)^3 & \Leftrightarrow T^3 + 4T^2 + 4T = T^3 + 3T^2 + 3 + 1 \\ & \Leftrightarrow T^2 + T - 1 = 0 \\ & \Leftrightarrow T = \frac{1 \pm \sqrt{5}}{2} \end{align} \] Comme \(T\) est une durée, donc positive, on en déduit qu’il a commencé à neiger il y a \(\frac{1+\sqrt{5}}{2}\).
Problème (pour les braves)
Motivation
Si on tire \(2n\) pièces (équilibrées) à pile ou face et qu’on note \(X\) le nombre de piles, le résultat le plus probable est \(X=n\).
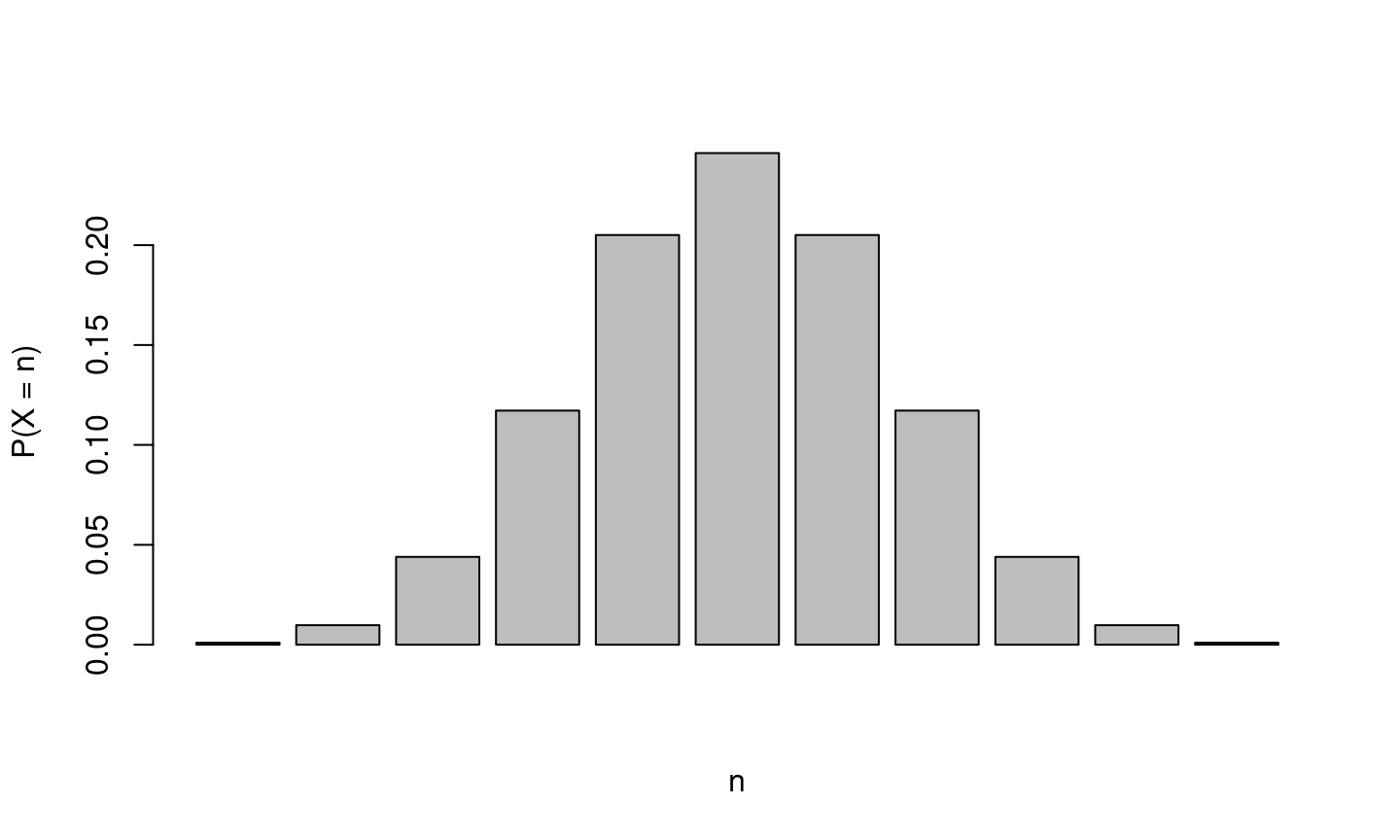 et on peut note \(p_n = P(X=n)\) la probabilité d’un tel évènement.
et on peut note \(p_n = P(X=n)\) la probabilité d’un tel évènement.
Préalable
A l’aide des distributions binomiales, montrer que \[ p_n = \frac{(2n)!}{2^{2n}(n!)^2} \] Cette formule est exacte mais pas très pratique, car on ne peut pas facilement comparer \(n!\) et \((2n)!\).
On va essayer d’y remédier avec la
Formule de Stirling
On va essayer d’utiliser nos connaissances pour trouver un équivalent de \(n!\) et démontrer la formule de Stirling: \[ n! \sim \sqrt{2\pi n} \left( \frac{n}{e} \right)^n \] On va procéder en deux temps:
- faire un développement asymptotique pour montrer que \[\ln(n!) = (n+\frac{1}{2})\ln(n) - n + C + o(1)\] pour un certain \(C > 0\) inconnu
- calculer \(C\) en étudiant les intégrales de Wallis.
Préalable
Avant de pouvoir faire le développement de \(\ln(n!)\) on va devoir établir quelques résultats préalables.
Formule de Taylor étendue
On suppose que \(f\) est concave, de classe \(\mathcal{C}^2\) sur \([a,b]\) et on note \(M\) un majorant de \(|f''|\) sur \([a,b]\). On va chercher un majorant de \[g(x) = f(x) - \left[ f(a) + (x-a) \frac{f(b) - f(a)}{b-a} \right]\] qui est la différence entre \(f\) et son approximation par une fonction linéaire sur \([a,b]\).
- Montrer que pour tout \(x\) dans \([a,b]\), \(g(x) = \int_a^x g'(u) du\) et \(g'(u) = \int_a^u f''(t)dt + g'(a)\)
- En déduire que \(g(x) = \int_{u=a}^{u=x} [ \int_{t=a}^{t=u} f''(t)dt + g'(a)]du\)
Formule de Taylor étendue (II)
- En utilisant le TAF puis la concavité de \(f\), montrer que \(g'(a) \leq f'(a) - f'(b)\)
- En utilisant l’IAF, montrer que \(g'(a) \leq M (b - a)\)
- Déduire des résultats précédents que \[ g(x) \leq M(x-a) \left[ \frac{x - a}{2} + (b-a)\right] \]
Formule de Taylor étendue (III)
- En déduire que \(\int_a^b g(u)du \leq M \frac{2(b - a)^3}{3}\)
- En calculant \(\int_a^b g(x)dx\), montrer que \[ \int_a^b f(x)dx - (b-a)\frac{f(a)+f(b)}{2} \leq M \frac{2(b - a)^3}{3} \] En particulier, si \(a = n\) et \(b = n+1\), on a \[ \int_n^{n+1} f(x)dx - \frac{f(n)+f(n+1)}{2} \leq \frac{2}{3}\max_{x \in [n, n+1]} |f''(x)| \] En faisant plus d’efforts, on pourrait remplacer le \(2/3\) par un \(1/12\) (valeur optimale).
Approximation de \(\ln(n!)\)
On pose \(u_n = \int_{n}^{n+1} \ln(x) dx - \frac{\ln(n) + \ln(n+1)}{2}\) et \(U_n = \sum_{i=1}^n u_n\).
- Vérifier que \(\ln(x)\) est concave
- Montrer que \(0 \leq u_n \leq \frac{2}{3n^2}\) pour tout \(n\)
- En déduire que \(U_n\) est croissante et majorée et donc converge vers une limite \(C\) (à ne pas déterminer)
- En déduire \[ \sum_{i=1}^n \ln(i) = \int_{1}^n \ln(x)dx + \frac{\ln(n)}{2} + C + o(1) \]
Digressions
On a fait beaucoup d’effort pour écrire un développement asymptotique de \(\ln(n!)\) alors qu’une simple comparaison somme-intégrale aurait déjà donné \[ \ln(n!) \sim n\ln(n) \] Mais ce développement n’est pas suffisamment précis pour obtenir un développement de \(n!\). En effet, on peut avoir \(\ln(n!) - n\ln(n) \to \pm \infty\) qui ne permet pas de passer à l’exponentielle (puisque \(e^\infty = +\infty\) et \(e^{-\infty} = 0\)).
Quelle précision est nécessaire? Il faut être capable de déterminer précisément l’exponentielle du terme de reste, qui doit donc être d’ordre \(o(1)\) puisque \(e^{o(1)} \to e^0 = 1\).
Digressions (suite)
On a le travail pour \(f(x) = \ln(x)\) mais le raisonnement marche pour n’importe quelle fonction \(f\). En utilisant le raisonnement précédent, on peut montrer que \[ \left| \int_{1}^n f(x)dx - \left[ \sum_{i=1}^{n} f(i) - \frac{f(1)+f(n)}{2}\right] \right| \leq \sum_{i=1}^n \frac{1}{6}\max_{x \in [i, i+1]} f''(x) \]
Pour peu qu’on soit capable de contrôler \(\sum_{i=1}^n \frac{1}{6}\max_{x \in [i, i+1]} f''(x)\) et de calculer \(\int_1^n f(x)dx\) , cette majoration permet souvent de donner une bonne approximation de \(\sum_i f(i)\).
Intégrales de Wallis
On sait désormais que \(n! = L \sqrt{n}(n/e)^n (1 + o(1))\) (avec \(L = e^C\) et \(e^{o(1)} = 1+ o(1)\)). Il nous reste donc à calculer \(L\).
On recourre pour ce faire aux intégrales de Wallis définies par \[ I_n = \int_{0}^{\pi/2} \cos^{n}(x)dx \]
Étude de \(I_n\)
- Calculer \(I_0\), \(I_1\), \(I_2\) et \(I_3\);
- À l’aide d’une IPP, montrer que \(I_{n+2} = \frac{n+1}{n+2} I_n\) pour tout \(n\);
- En déduire que \(I_{2n} = \frac{\pi}{2} \frac{(2n)!}{(2^n n!)^2}\) (ça vous rappelle quelque chose?)
- Montrer que \(I_{2n} I_{2n+1} = \frac{\pi}{2(2n+1)}\) pour tout \(n\);
- Montrer que \(I_n\) est décroissante;
- Montrer que \(n (I_{2n})^2 \to \frac{\pi}{4}\) quand \(n \to \infty\)
- En déduire la valeur de \(L\) et un équivalent de \(p_n\)
Conclusion
On vient de montrer que \[ p_n \sim \frac{1}{\sqrt{\pi n}} \quad \text{et} \quad n! \sim \sqrt{2\pi n} \left(\frac{n}{e}\right)^n \]
Les étudiants attentifs pourront remarquer que les intégrales de Wallis suffisaient en fait pour calculer un équivalent de \(p_n\)…
La formule de Stirling est en fait un résultat plus fort qui peut être utilisé dans d’autres circonstances, par exemple pour calculer un équivalent de n’importe proba de la forme \(P(X = k)\) quand \(k=\lfloor \alpha n \rfloor\) avec \(\alpha \in (0, 1)\) et \(X \sim \mathcal{B}(n, 1/2)\)