30 Septembre 2019
Introduction
Plan de la leçon
- L’ensemble \(\mathbb{C}\)
- Exponentielle complexe
- Applications à la trigonométrie
- Équations dans \(\mathbb{C}\) (ensemble, en classe)
Objectifs
- Manipuler des nombres complexes (addition, multiplication)
- Choisir entre forme algébrique et forme exponentielle
- Avoir une visio géométrique de \(\mathbb{C}\)
- Connaître les formules de Moivre et d’Euler
- Savoir retrouver les égalités trigonométriques
- Trouver une racine carré dans \(\mathbb{C}\).
Les nombres complexes
Définition et généralités
L’ensemble \(\mathbb{C}\) contient tous les réels ainsi qu’un nombre, noté \(i\) qui vérifie \(i^2 = -1\). Pour tout \(z \in \mathbb{C}\), il existe un unique couple \((a, b) \in \mathbb{R}^2\) tel que: \[z = a + i \times b\] Tout nombre réel \(x\) s’écrit alors \[x = x + i \times 0\] Les nombres complexes s’additionnent et se manipulent de la façon suivante: pour tous réels \(a, a', b, b'\) on a \[\begin{eqnarray} (a+ib) + (a'+ib') & = & (a+a') + i(b+b')\\ (a+ib) \times (a'+ib') & = & (aa' -bb') + i(ab' + a'b) \end{eqnarray}\]
Terminologie
L’écriture d’un complexe \(z\) sous forme \(z = a + ib\) (avec \(a\) et \(b\)
- Le nombre \(a\) s’appelle partie réelle de \(z\) et se note \(Re(z)\)
- Le nombre \(b\) s’appelle partie imaginaire de \(z\) et se note \(Im(z)\)
Complexe conjugué
Soit \(z = a + ib\) un nombre complexe sous forme algébrique. On appelle nombre complexe conjugué, noté \(\bar{z}\), le complexe \[\bar{z} = a -ib\]
Remarques - Un complexe \(z\) est un réel si et seulement si \(Im(z) = 0\). - Un complexe \(z\) dont la partie réelle est nulle (\(Re(z) = 0\)) est dit imaginaire pur. On note \(i\mathbb{R}\) l’ensemble des imaginaires purs.
Conjugaison, réels et imaginaire purs
- On a \(z + \bar{z} = 2 Re(z)\) et \(z - \bar{z} = 2i Im(z)\)
- \(z\) est réel pur si et seulement si \(z = \bar{z}\) et imaginaire pur si et seulement si \(z = -\bar{z}\)
- \(Re(z+z') = Re(z) + Re(z')\) et \(Im(z + z') = Im(z) + Im(z')\)
- Si \(\lambda \in \mathbb{R}\), alors \(Re(\lambda z) = \lambda Re(z)\) et \(Im(\lambda z) = \lambda Im(z)\). Ce n’est pas vrai en général si \(\lambda \in \mathbb{C}\).
Opérations sur les complexes
On a les mêmes règles d’opérations dans \(\mathbb{C}\) que dans \(C\) (et même un peu plus avec la conjugaison)
- \(z + z'\) = \(z' + z\) et \(zz' = z'z\)
- \(z + (z' + z'') = (z + z') + z''\) et \(z(z'z'') = (zz')z''\)
- \(z + 0 = z\), \(z \times 1 = z\) et \(z \times 0 = 0\)
- \(\overline{z+ z'} = \bar{z} + \bar{z'}\) et \(\overline{zz'} = \bar{z} \times \bar{z'}\)
- \(z \times (z' + z'') = zz' + zz''\)
- Si \(z = a+ib\) sous forme algébrique, \(z\bar{z} = a^2 + b^2\)
- Si \(z = a+ib \neq 0\), \(z^{-1} = \frac{a - ib}{a^2 + b^2}\)
Écriture algébrique: exercices
- \(z_1 = (2 -i)(4+2i)\)
- \(z_2 = \frac{z_1}{2+i}\)
- \(z_3 = \overline{z_1 z_2}\)
Interprétation géométrique
On peut voir un nombre complexe \(z\) comme un couple \((a, b)\) de nombres réels. On peut donc représenter les complexes comme des points dans le plan \(\mathcal{P}\) muni du repère orthonormé \((O, \vec{i}, \vec{j})\).
Soit \(M\) un point de coordonnées \((a, b)\) dans le plan \(\mathcal{P}\) muni du repère \((O, \vec{i}, \vec{j})\). On associe à \(M\) le nombre complexe \(z_M = a + ib\). \(z_M\) est appelé affixe (complexe) du point \(M\).
Réciproquement, à tout complexe \(z = a + ib\), on peut associer son point image \(M(z) \in \mathcal{P}\) de coordonnées \((a, b)\).
Enfin, si \(\vec{\alpha}\) est un vecteur du plan de coordonnées \((a, b)\), on lui associe son affixe complexe \(z_{\vec{\alpha}} = a + ib\).
Pour les propriétés qui suivent, faites des dessins pour les visualiser.
Interprétation géométrique (II)
Soit \(A, B\) deux points du plan, on a \[z_\vec{AB} = z_B - z_A\]
- \(z \in \mathbb{R} \Leftrightarrow M(z)\) est sur l’axe des abscisses
- \(z \in i\mathbb{R} \Leftrightarrow M(z)\) est sur l’axe des ordonnées
- Soit \(\vec{\alpha}\) et \(\vec{\beta}\) d’affixes respectives \(z_\alpha\) et \(z_\beta\). Le complexe \(z_\alpha + z_\beta\) est l’affixe de \(\vec{\alpha} + \vec{\beta}\). Autrement dit, \(z_{\alpha + \beta} = z_{\alpha} + z_{\beta}\).
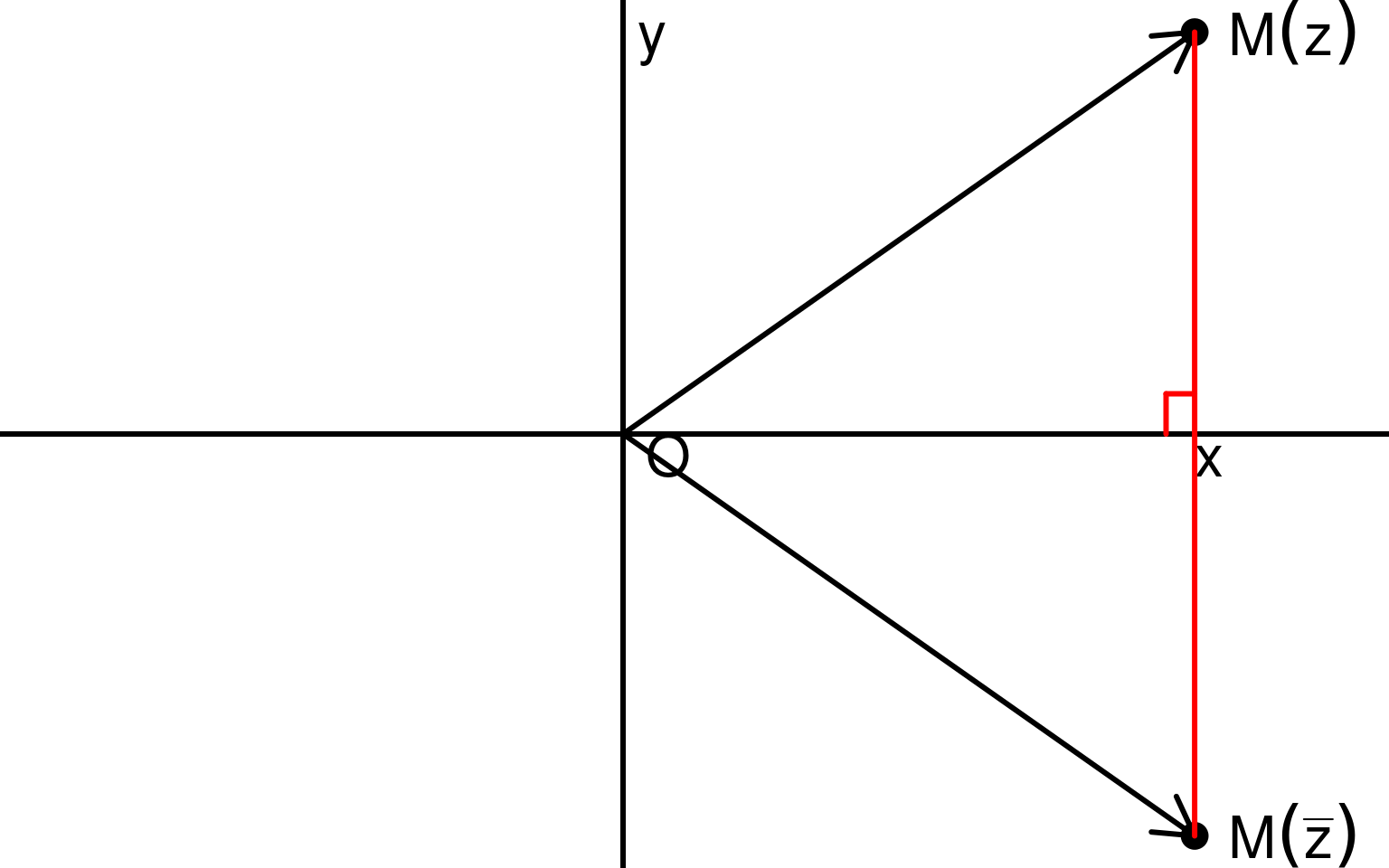
- Soit \(z \in \mathbb{C}\) et \(M(z)\) son point image. Alors le point \(M(\bar{z})\), image de \(\bar{z}\) est l’image de \(M(z)\) par la symmétrie d’axe \((Ox)\)
Interprétation géométrique du conjugué
Interprétation géométrique: exercices
:
- \(A\), \(B\) et \(C\) sont alignés si et seulement si \(\frac{b-a}{c-a} \in \mathbb{R}\)
- Le triangle \(ABC\) est rectangle en \(A\) si et seulement si \(Re((b -a) (\overline{c - a})) = 0\)
Dans les deux cas, on pourra faire un dessin pour avoir une intuition géométrique des conditions (vecteurs colinéaires ou perpendiculaires) et essayer de les traduires en termes de condition sur les nombre complexes.
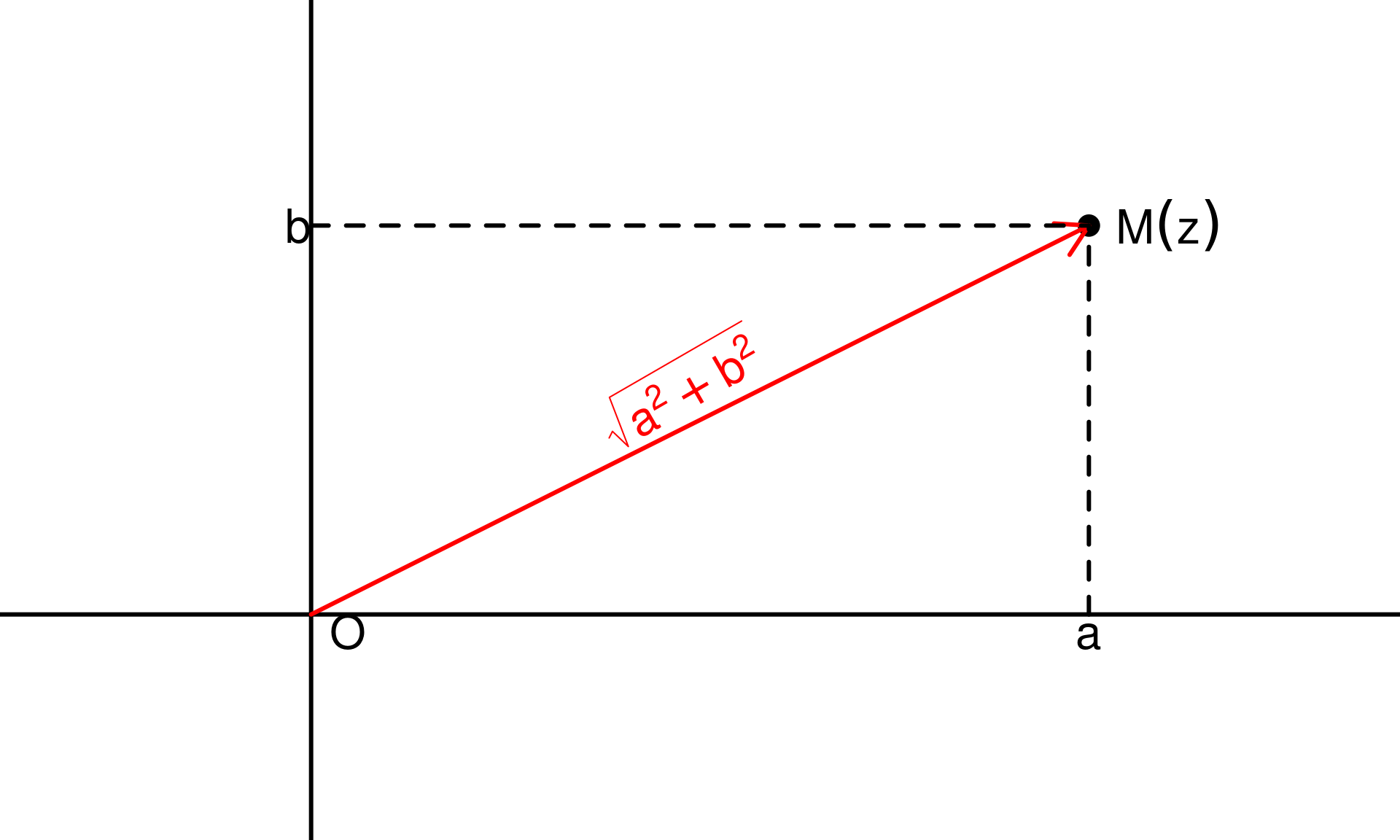
Module d’un complexe
Soit \(z = a + ib\) un nombre complexe sous forme algébrique. Le module de \(z\), noté \(|z|\) est la distance entre le point \(O\) (d’affixe \(0\)) et le point \(M(z)\) (d’affixe \(z\)), c’est à dire \[|z| = OM(z) = \sqrt{a^2 + b^2}\] De même, si \(z\) est l’affixe d’un vecteur \(\vec{\alpha}\), alors \(|z| = \|\vec{\alpha}\|\) où \(\|\vec{\alpha}\|\) désigne la norme du vecteur \(\vec{\alpha}\).
Le module est la généralisation à \(\mathbb{C}\) de la valeur absolue sur \(\mathbb{R}\). C’est pour ça qu’on utilise la même notation.
Module d’un complexe: géométrie
Module d’un complexe: propriétés
- \(|z| \geq 0\)
- \(|z| = 0 \Leftrightarrow z = 0\)
- \(|z| \geq |Re(z)|\) avec égalité si et seulement si \(z \in \mathbb{R}\)
- \(|z| \geq |Im(z)|\) avec égalité si et seulement si \(z \in i\mathbb{R}\)
- \(|z| = |\bar{z}|\), \(z\bar{z} = |z|^2\)
- \(|zz'| = |z||z'|\) et pour tout \(n \in \mathbb{Z}\), \(|z^n| = |z|^n\)
- \(|z - z'| = \|\vec{M(z)M(z')}\|\)
Module d’un complexe: exercices
On rappelle que la sommes de réels positifs est nulle si et seulement si tous ces réels sont nuls: \[\forall (x_1, x_2, \dots, x_n) \in \mathbb{R}_+^n, x_1 + \dots + x_n = 0 \Leftrightarrow x_1 = \dots x_n = 0\]
- Démontrer les inégalités et égalités de la proposition précédente (en passant par les formes algébriques de \(z\) et \(z'\)).
- Déterminer les \(z \in \mathbb{C}\) tels que \(|z - i| = |z + i|\) (on peut essayer d’avoir une interprétation géométrique pour cet exercice)
- Déterminer les \(z \in \mathbb{C}\) tels que \(z\), \(1/z\) et \(1-z\) ont le même module (on peut essayer de déterminer \(|z|\) avant d’avoir une interprétation géométrique)
Inégalité triangulaire
Soit \(z\) et \(z'\) deux complexes. On a \[ |z + z'| \leq |z| + |z'|\]
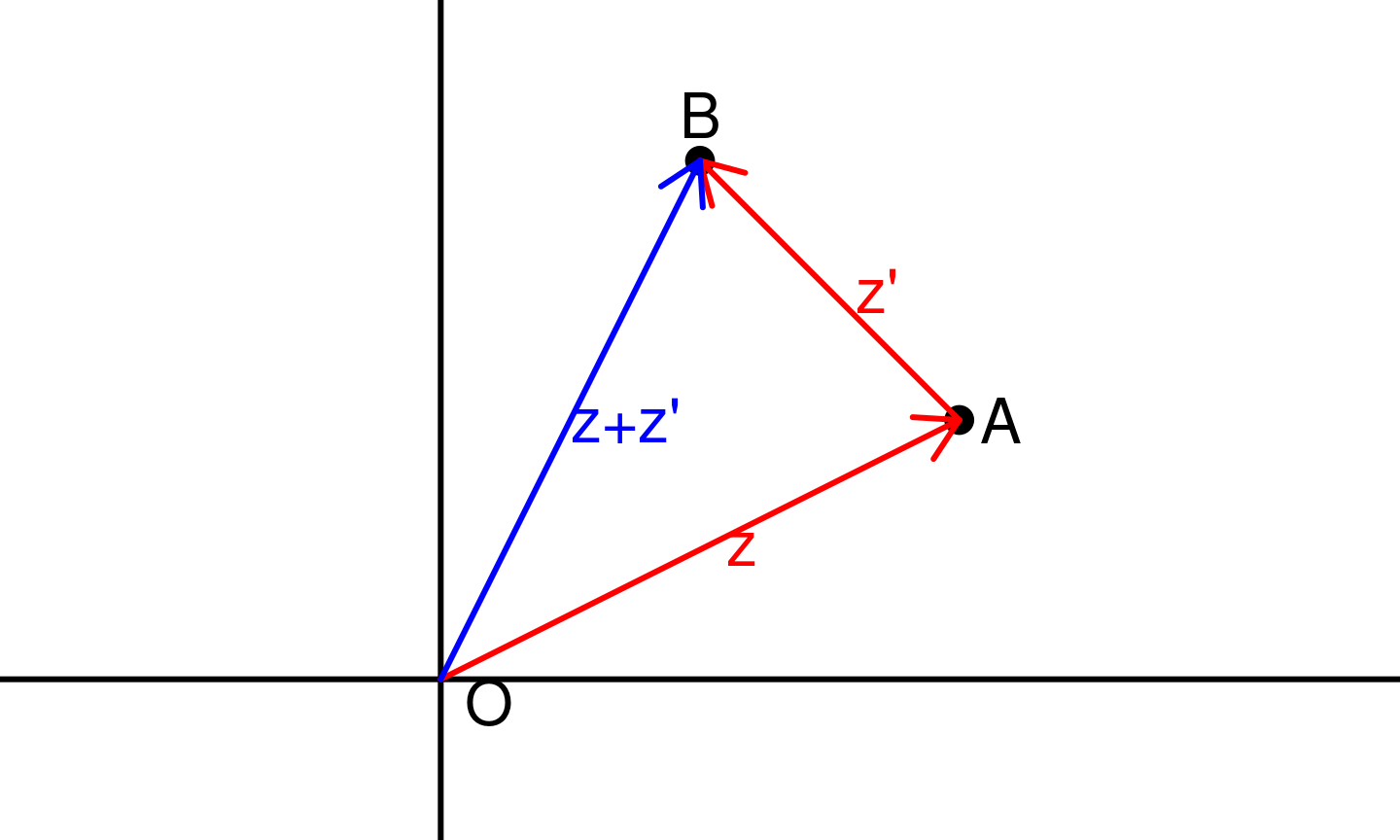
Inégalité triangulaire: preuve géométrique
Soit \(O\) le point d’affixe \(0\), \(A\) celui d’affixe \(z\) et \(B\) celui d’affixe \(z+z'\).
L’inégalité triangulaire dans le triangle \(ABO\) donne \[ OB \leq OA + AB \]
Or \(OB = |z + z'|\), \(OA = |z|\) et \(AB = |z'|\) donc on a bien \[ |z + z'| \leq |z| + |z'|\]
Exponentielle complexe
Nombres complexes de module 1
L’ensemble des nombres complexes de module \(1\) se note \(\mathbb{U}\). Il correspond géométriquement à l’ensemble des affixes des points du cercle unité (de centre \(O\) et de rayon \(1\)).
Soit \(z\) un nombre de complexe de module \(1\), il existe un réel \(\theta\) (en fait une infinité) tel que \[z = \cos(\theta) + i\sin(\theta)\]
C’est immédiat avec ce qu’on a vu en trigonométrie. Comme \(z = a + ib\) est de module \(1\) on a \(a^2 + b^2 = 1\) et \(a\) et \(b\) peuvent donc s’écrire comme le \(\cos\) et le \(\sin\) d’un angle \(\theta\) bien choisi.
Argument d’un nombre complexe
Soit \(z\) un nombre complexe
Remarques - Il y a une infinité d’arguments, l’argument n’est défini qu’à \(2\pi\) près. - On parle d’un argument, pas de l’argument d’un complexe - Si on se restreint à un intervalle \(I\) de longueur \(2\pi\) (par exemple \(]-\pi, \pi]\)), l’argument est bien unique dans \(I\).
Argument d’un nombre complexe: propriété
- \(\theta + \theta'\) est un argument de \(zz'\)
- \(-\theta\) est un argument de \(1/z\) et de \(\bar{z}\)
- \(\theta-\theta'\) est un argument de \(z/z'\). Si deux vecteurs \(\vec{u}\) et \(\vec{u'}\) ont pour affixe \(z\) et \(z'\), alors \(\text{arg}(z/z')\) est une mesure de l’angle orienté \((\vec{u}, \vec{u'})\)
Lien avec les rotations
On rappelle que la rotation \(R(O, \alpha)\) est l’application de \(\mathcal{P} \to \mathcal{P}\) qui à tout point \(M\) associe le point \(M'\) qui vérifie: - \(OM = OM'\) - \((\vec{OM}, \vec{OM'}) = \alpha\)
On sait que \(\mathcal{P}\) est identifié à \(\mathbb{C}\). On peut donc se demander s’il existe un lien entre l’affixe \(z\) de \(M\) et celle \(z'\) de \(M'\).
La réponse est oui. Si \(z_\alpha\) est un nombre complexe tel que \(|z_\alpha| = 1\) et que \(\alpha\) est un argument de \(z_\alpha\), alors \(z' = z_\alpha z\). Autrement dit, multiplier par un nombre complexe de module \(1\) et d’argument \(\alpha\) revient à faire une rotation de centre \(O\) et d’angle \(\alpha\) sur les images.
Argument: exercices
- Écrire sous forme algébrique \(z = \frac{1+i}{a + ib}\) où \((a, b) \neq (0, 0)\) est un couple de réels.
- Écrire sous forme algébrique et trouver un argument et le module de \(z_1 = \frac{-4}{1 + i\sqrt{3}}\) et \(z_2 = (1+i)^3\)
- Déterminer le module et un argument des nombres complexes suivants: \[z_0 = i\sin(3\pi / 8), z_1 = \frac{\sqrt{6} + i\sqrt{2}}{2}, z_2 = 1 + i, z_3 = \frac{z_1}{z_2}\]
Exponentielle complexe
Soit \(\theta \in \mathbb{R}\), on note \[e^{i\theta} = \cos(\theta) + i\sin(\theta)\]
Soit \(\theta, \theta' \in \mathbb{R}\), on a \[e^{i\theta + i\theta'} = e^{i(\theta + \theta')} = e^{i\theta} \times e^{i\theta'}\]
Remarques La définition de \(e^{i\theta}\) peut sembler arbitraire mais la proposition précédente montre que c’est la “bonne” définition: c’est celle qui étend les propriétés de l’exponentielle des réels purs aux imaginaires purs.
Exponentielle complexe et conjugaison, argument
Soit \(\rho > 0\) et \(\theta \in \mathbb{R}\), on a \[\overline{\rho e^{i\theta}} = \rho e^{-i\theta}\]
Soit \(z\) un complexe non nul et \(\theta\) un réel. \(\theta\) est un argument de \(z\) si et seulement \(z = |z|e^{i\theta}\)
Soit \(z\) un complexe non nul. Il existe un couple \((\rho, \theta) \in \mathbb{R}_+^\star \times \mathbb{R}\) tel que \[ z= \rho e^{i\theta}\]
- Remarque Il existe une infinité de \((\rho, \theta)\) mais ils sont liés les uns aux autres, comme le montre la proposition suivante.
Forme exponentielle
Soit \(z, z'\) deux nombres complexes non nuls tels que \[ z= \rho e^{i\theta} \text{ et } z= \rho' e^{i\theta'} \text{ avec } \rho, \rho' > 0\] Alors, on a \[ z = z' \Leftrightarrow \begin{cases} \rho = \rho' \\ \exists k \in \mathbb{Z} \text{ tel que } \theta' = \theta + 2k\pi \end{cases}\]
- Si \(\theta\) et \(\theta'\) sont distincts dans \([0, 2\pi[\) (ou n’importe quel intervalle de longueur \(2\pi\)), alors \(e^{i\theta} \neq e^{i\theta'}\)
- Soit \(z \in \mathbb{C}\), non-nul et \((\rho, \theta) \in \mathbb{R}_+^\star \times \mathbb{R}\). Alors \(z = \rho e^{i\theta}\) si et seulement si \(|z| = \rho\) et \(\theta\) est un argument de \(z\). Cette notation s’appelle la forme exponentielle de \(z\).
Exponentielle complexe
Soit \(z = a+ib\) un nombre complexe sous forme algébrique. On pose \[ e^z= e^a e^{ib} = e^a (\cos(b) + i\sin(b)) \]
- \(e^{z+z'} = e^z \times e^{z'}\)
- \((e^z)^n = e^{nz}\)
Remarques La définition et la proposition montre que l’exponentielle complexe étend bien l’exponentielle réelle de façon cohérente sur \(\mathbb{C}\) (on l’avait déjà vu pour \(i\mathbb{R}\))
Exponentielle complexe (II)
- \(|e^{z}| = e^{Re(z)}\)
- \(e^z = 1\) si et seulement si il existe \(k \in \mathbb{Z}\) tel que \(z = 2ik\pi\)
Remarque Contrairement aux nombres réels positifs, \(z^x\) n’est pas bien défini quand \(z\) est complexe (alors que pour \(a > 0\), on a \(a^x = e^{x\ln(a)})\). On retiendra donc que \(z^x\) (avec \(z\) complexe) n’est bien défini que pour \(x \in \mathbb{Z}\).
Exponentielle complexe: exercices
Dans les exercices suivants, l’objectif est de se ramener à des sommes connues (Sommes des termes d’une suite géométrique, Binôme de Newton). On peut par exemple essayer de calculer \(A_n + iB_n\) avant d’isoler ses parties réelles et imaginaires. On peut aussi noter que \(\cos(k\theta) + i\sin(k\theta) = (e^{i\theta})^k\).
Calculer, pour \(n \in \mathbb{N}\) et \(\theta \in \mathbb{R}\):
- \(A_n = \sum_{k=0}^n \cos(k\theta)\) et \(B_n = \sum_{k=0}^n \sin(k\theta)\)
- \(A_n = \sum_{k=0}^n {n \choose k} \cos(k\theta)\) et \(B_n = \sum_{k=0}^n {n \choose k} \sin(k\theta)\)
Nombres complexes et trigonométrie
Application à la trigonométrie
On l’a vu dans la définition de l’exponentielle complexe mais il existe un lien fort entre les fonctions trigonométriques et l’exponentielle complexe. Ce lien est formalisé par les formules d’Euler
Soit \(\theta\) un nombre réel. On a \[\cos(\theta) = \frac{e^{i\theta} + e^{-i\theta}}{2} \text{ et } \sin(\theta) = \frac{e^{i\theta} - e^{-i\theta}}{2i}\]
Un autre lien fort qui existe est la formule de Moivre:
Soit \(\theta\) un nombre réel et \(n \in \mathbb{Z}\). On a \[(\cos(\theta) + i\sin(\theta))^n = (e^{i\theta})^n = \cos(n\theta) + i\sin(n\theta)\]
Application à la trigonométrie (II)
Il est plus aisé de retrouver les formules d’additions à partir de la définition de l’exponentielle complexe que de les apprendre par coeur. En effet:
\[\begin{align} \cos(a+b) & = Re(e^{i(a+b)}) = Re(e^{ia} \times e^{ib}) \\ & = Re((\cos(a)\cos(b) - \sin(a)\sin(b)) \\ & \quad + i(\cos(a)\sin(b) + \sin(a)\cos(b)) ) \\ & = \cos(a)\cos(b) - \sin(a)\sin(b) \\ \end{align}\]
On montre de même que \[ \sin(a+b) = \cos(a)\sin(b) + \sin(a)\cos(b)\]
Toutes les autres formules en découlent.
Linéarisation
L’idée est d’exprimer \(\cos^n(x)\sin^p(x)\) pour \(x \in \mathbb{R}\) et \(n,p \in \mathbb{N}\) en fonction des \(\cos(kx)\) et des \(\sin(kx)\). Pour ce faire on utilise les formules d’Euler.
On commence par écrire \[\cos^n(x)\sin^p(x) = \left( \frac{e^{i\theta} + e^{-i\theta}}{2}\right)^n \left( \frac{e^{i\theta} - e^{-i\theta}}{2i} \right)^p\]
Ensuite, on développe (en utilisant le binôme de Newton) et on utiliser les formules d’Euler dans l’autre sens pour simplifier.
Linéarisation: Exemple
On chercher à linéariser \(\cos^3(x)\)
\[\begin{align} \cos^3(x) & = \left( \frac{e^{ix} + e^{-ix}}{2}\right)^3 \\ & = \frac{1}{8}\left(e^{i3x} + 3e^{i2x}e^{-ix} + 3e^{ix}e^{-i2x} + e^{-i3x}\right) \\ & = \frac{1}{8} \left(e^{i3x} + 3e^{ix} + 3e^{-ix} + e^{-i3x}\right) \\ & = \frac{1}{8} \left(e^{i3x} + e^{-i3x} + 3(e^{ix} + e^{-ix})\right) \\ & = \frac{1}{8} \left(2\cos(3x) + 6\cos(x)\right) = \frac{1}{4}(3\cos(x) + \cos(3x)) \\ \end{align}\]
Transformation de \(\cos(nx)\)
C’est la transformation inverse de la précédente. On veut exprimer \(\cos(nx)\) en fonction de \(\cos(x)\) et \(\sin(x)\). Pour cela, on applique la formule de Moivre: \[\begin{align} \cos(nx) & = Re(\cos(nx) + i\sin(nx)) \\ & = Re((\cos(x) + i\sin(x))^n) \end{align} \] Il suffit alors de développer en utilisant le binôme de Newton et de ne garder que la partie réelle.
Transformation de \(\cos(nx)\): exemple
Pour \(n = 3\), on a \[\begin{align} (\cos(x) + i\sin(x))^3 & = \cos^3(x) + 3i\cos^2(x)\sin(x) \\ & \quad - 3\cos(x)\sin^2(x) -i\sin^3(x) \\ & = \cos^3(x) - 3\cos(x)\sin^2(x) \\ & \quad + i(3\cos^2(x)\sin(x) - \sin^3(x)) \\ \end{align} \]
On en déduit \[\begin{align} \cos(3x)& = \cos^3(x) - 3\cos(x)\sin^2(x) \\ \sin(3x)& = 3\cos^2(x)\sin(x) - \sin^3(x) \\ \end{align} \]
Linéarisation, transformation: exemples
- Linéariser \(\sin^4(x)\)
- Exprimer \(\cos(5x)\) en fonction de \(\cos(x)\) (uniquement \(\cos(x)\))
Recherche d’une raciné carrée dans \(\mathbb{C}\)
Calcul d’une racine carrée complexe
Soit \(Z\) un nombre complexe, on cherche à calculer une racine carrée de \(Z\) c’est à dire un nombre complexe \(z\) tel que \(z^2 = Z\).
Comme dans \(\mathbb{R}\), si \(z\) est solution, alors \(-z\) mais contrairement à \(\mathbb{R}\), on ne peut pas parler de la racine carrée puisque la condition \(z > 0\) n’a pas de sens pour un complexe.
Racine carrée dans \(\mathbb{C}\)
Soit \(Z\) un nombre complexe
Si \(Z = \rho e^{i\theta}\) avec \(\rho \geq 0\), ces deux solutions sont: \[z_1 = \sqrt{\rho}e^{i\theta/2} \text{ et } z_2 = -z_1 = -\sqrt{\rho}e^{i\theta/2}\]
Si \(Z\) est donné sous forme algébrique, il faut faire plus d’efforts…
Calcul d’une racine carrée complexe: forme algébrique
Si \(Z\) est donné sous forme algébrique \(Z = A + iB\) (avec \(A, B\) réels), on va chercher les racines carrés \(z\) sous forme algébrique \(z = a + ib\) en utilisant 2 propriétés:
- \(z^2 = Z\)
- \(|z|^2 = |Z|\)
Calcul d’une racine carrée complexe: forme algébrique
La première (\(z^2 = Z\)) donne: \[\begin{align} z^2 = A + iB & \Leftrightarrow (a^2-b^2) + 2iab = A + iB \\ & \Leftrightarrow \begin{cases} a^2 - b^2 & = & A \\ 2ab & = & B \end{cases} \end{align} \]
La deuxième (\(|z|^2 = |Z|\)) donne \[a^2 + b^2 = \sqrt{A^2 + B^2}\]
Calcul d’une racine carrée complexe: forme algébrique
On peut résoudre le premier système: \[ \begin{align*} \begin{cases} a^2 - b^2 & = & A \\ a^2 + b^2 & = & \sqrt{A^2 + B^2} \end{cases} & \Leftrightarrow \begin{cases} 2a^2 & = & \sqrt{A^2 + B^2} + A \\ 2b^2 & = & \sqrt{A^2 + B^2} - A\end{cases} \\ & \Leftrightarrow \begin{cases} a & = & \pm \sqrt{\frac{\sqrt{A^2 + B^2} + A}{2}} \\ b & = & \pm \sqrt{\frac{\sqrt{A^2 + B^2} - A}{2}} \end{cases} \end{align*} \]
On a donc \(4\) possibilités pour \((a, b)\). Le signe de \(B = 2ab\) permet de n’en conserver que deux des 4.
Calcul d’une racine carrée complexe: Exemple
On essaie de calculer les racines carrés de \(5 - 12i\). Il n’y a pas de forme exponentielle intéressante pour ce complexe donc on passe par la forme algébrique. On cherche une racine carré \(z = a + ib\) sous forme algébrique. On a d’une part: \[ \begin{eqnarray*} z^2 = 5 - 12i & \Leftrightarrow & (a^2 - b^2) + 2iab = 5 - 12i \\ & \Leftrightarrow & \begin{cases} a^2 - b^2 & = & 5 \\ 2ab & = & -12 \end{cases} \end{eqnarray*}\] Et d’autre part \(|z|^2 = a^2 + b^2 = |5 - 12i| = \sqrt{25 + 144} = \sqrt{169} = 13\).
Calcul d’une racine carrée complexe: Exemple
On doit donc résoudre le système: \[\begin{cases} a^2 - b^2 & = & 5 \\ a^2 + b^2 & = & 13 \end{cases} \Leftrightarrow \begin{cases} a^2 & = & 9 \\ b^2 & = & 4 \end{cases}\]
Qui donne \(a = \pm 3\) et \(b = \pm 2\). Comme \(ab = 6 < 0\), les deux solutions sont: \[z_1 = 3-2i \text{ et } z_2 = -3 + 2i\].
Trinôme de degré 2 dans C
Soit \((a, b, c) \in \mathbb{C}\) avec
En notant \(\alpha\) une racine carrée de \(\Delta\) (qui existe toujours), les solutions de \((E)\) sont: \[ z_1 = \frac{-b + \alpha}{2a} \text{ et } z_1 = \frac{-b - \alpha}{2a}\]
Remarque Contrairement aux équations de degré 2 dans \(\mathbb{R}\), les équations de degré \(2\) dans \(\mathbb{C}\) ont toujours deux solutions (potentiellement confondues).
Trinôme de degré 2 dans C: racines
Avec les notations précédentes, on a \(z_1 z_2 = c/a\) et \(z_1 + z_2 = - b/a\)
Remarques
- La proposition précédente est utile pour trouver des nombres dont on connaît la somme \(S\) et le produit \(P\): il suffit de trouver les racines du polynôme \(X^2 -SX + P\).
- Un usage plus pragmatique consiste à vérifier vos calculs: une fois trouvées les deux racines d’un trinôme en passant par le discriminant, vous pouvez vérifier leur cohérence avec la proposition précédente.
- Un autre usage pragmatique consiste à accélérer les calculs: si vous trouvez une racine évidente \(z_1\), l’autre est forcément égale à \(c/(az_1)\). Par exemple \(1\) est racine évidente de \(X^2 - 3X + 2\), l’autre est forcément \(2\).
Exercices
La Places des Vosges a une superficie de 19600 m\(^2\) et un périmètre de 560 mètres. Quelles sont ses dimensions?
On note \(l\) et \(L\) les dimensions la place. D’après l’énoncé \(lL = 19600\) et \(2(l+L) = 560\) donc \(l+L = 280\). On sait que \(l\) et \(L\) sont solutions de l’équation (d’inconnue \(x\)): \[(x-l)(x-L) = 0\] Cette équation peut se réécrire \[x^2 - (l+L)x +lL = 0\]
Exercices
En substituant avec les valeurs de l’énoncé, \(l\) et \(L\) sont solutions de l’équation \[x^2 - 280x + 19600 = 0\] En résolvant, on obtient \(l=L=140\). On pourrait pu aller plus vite en utilisant l’information que la place des Vosges est carrée…